题目内容
双曲线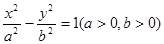
的左、右焦点分别为F1、F2，过点 F1作倾斜角为30°的直线l，l与双曲线的右支交于点P，若线段PF1的中点M落在y轴上，则双曲线的渐近线方程为 （ ）
A． | B． |
C． | D． |
C
解析试题分析：连接MF2，由过点 PF1作倾斜角为30°，线段PF1的中点M落在y轴上得：|MF1|=|MF2|═|PM|=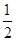
|PF1|，∴△PMF2为等边三角形，△PF1F2为直角三角形，因为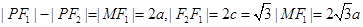
所以双曲线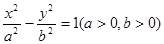
的渐近线方程为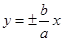
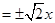,故选C.
考点：双曲线的简单几何性质
点评：本题考查直线与圆锥曲线的位置关系，关键是对双曲线定义的灵活应用及对三角形△PMF2为等边三角形，△PF1F2为直角三角形的分析与应用，属于难题．
练习册系列答案
名校课堂系列答案
相关题目
抛物线y=x2在点M（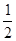
，
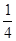）处的切线的倾斜角是（ ）
| A．30° | B．45° | C．60° | D．90° |
椭圆
的两焦点之间的距离为
A． | B． | C． | D． |
的左右焦点分别为
，若椭圆
上恰好有6个不同的点
，使得
为等腰三角形，则椭圆
右支上一点，
分别为双曲线的左、右焦点，I为△
的内心，若
成立，则
的值为（ ）
，它的一个焦点为F1，则满足
为等边三角形的椭圆的离心率是（ ）
设已知椭圆
＋
＝1(a>b>0)的一个焦点是圆x2＋y2－6x＋8＝0的圆心，且短轴长为8，则椭圆的左顶点为( )
| A．(－3，0) | B．(－4，0) | C．(－10，0) | D．(－5，0) |
已知椭圆的长轴长是短轴长的
倍，则椭圆的离心率等于
A． | B． | C． | D． |
已知函数
是偶函数，则函数的图象与y轴交点的纵坐标的最大值为：（ ）
| A．-4 | B．2 | C．3 | D．4 |