题目内容
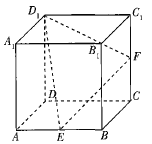
【题目】如图,在棱长为12的正方体![]() 中,已知E,F分别为棱AB,
中,已知E,F分别为棱AB,![]() 的中点,若过点
的中点,若过点![]() ,E,F的平面截正方体
,E,F的平面截正方体![]() 所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面
所得的截面为一个多边形,则该多边形的周长为________,该多边形与平面![]() ,ABCD的交线所成角的余弦值为________.
,ABCD的交线所成角的余弦值为________.
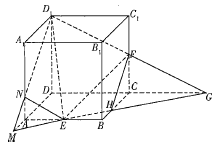
【答案】![]()
![]()
【解析】
延长DC,与![]() 的延长线交于点G,连接EG,交BC于点H,延长GE,与DA的延长线交于点M,连接
的延长线交于点G,连接EG,交BC于点H,延长GE,与DA的延长线交于点M,连接![]() ,交
,交![]() 于点N.连接NE,FH,作出截面多边形,由此易求该截面多边形的周长;多边形与平面
于点N.连接NE,FH,作出截面多边形,由此易求该截面多边形的周长;多边形与平面![]() ,ABCD的交线分别为
,ABCD的交线分别为![]() 与
与![]() ,由面面平行的性质定理得
,由面面平行的性质定理得![]() ∥
∥![]() ,则
,则![]() 为多边形与平面
为多边形与平面![]() ,ABCD的交线所成的角或其补角,利用余弦定理计算
,ABCD的交线所成的角或其补角,利用余弦定理计算![]() 即可.
即可.
如图,延长DC,与![]() 的延长线交于点G,连接EG,交BC于点H,延长GE,与DA的
的延长线交于点G,连接EG,交BC于点H,延长GE,与DA的
延长线交于点M,连接![]() ,交
,交![]() 于点N.连接NE,FH,
于点N.连接NE,FH,
因为正方体![]() 的棱长为12,
的棱长为12,
所以![]() .
.
因为![]() ∥
∥![]() ,
,
所以![]() ,
,
所以![]() ,
,
所以![]() ,
,
同理可得![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
易知![]() ,所以
,所以![]() ,
,
又![]() ,解得
,解得![]() ,
,
所以![]() ,
,![]() ,
,
则该多边形的周长为![]() .
.
由面面平行的性质定理得![]() ∥
∥![]() ,
,
则![]() 为多边形与平面
为多边形与平面![]() ,ABCD的交线所成的角或其补角.
,ABCD的交线所成的角或其补角.
因为![]() ,所以
,所以![]() ,
,
所以该多边形与平面![]() ,ABCD的交线所成角的余弦值为
,ABCD的交线所成角的余弦值为![]() .
.
故答案为:![]() ;
;![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为进一步深化“平安校园”创建活动,加强校园安全教育宣传,某高中对该校学生进行了安全教育知识测试(满分100分),并从中随机抽取了200名学生的成绩,经过数据分析得到如图1所示的频数分布表,并绘制了得分在![]() 以及
以及![]() 的茎叶图,分别如图23所示.
的茎叶图,分别如图23所示.
成绩 |
|
|
|
|
|
|
|
频数 | 5 | 30 | 40 | 50 | 45 | 20 | 10 |
图1
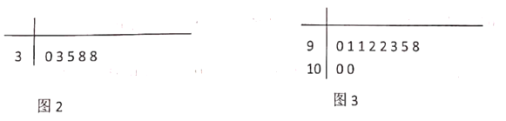
(1)求这200名同学得分的平均数;(同组数据用区间中点值作代表)
(2)如果变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() “近似满足正态分布
“近似满足正态分布![]() 的概率分布”.经计算知样本方差为210,现在取
的概率分布”.经计算知样本方差为210,现在取![]() 和
和![]() 分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布
分别为样本平均数和方差,以样本估计总体,将频率视为概率,如果该校学生的得分“近似满足正态分布![]() 的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
的概率分布”,则认为该校的校园安全教育是成功的,否则视为不成功.试判断该校的安全教育是否成功,并说明理由.
(3)学校决定对90分及以上的同学进行奖励,为了体现趣味性,采用抽奖的方式进行,其中得分不低于94的同学有两次抽奖机会,低于94的同学只有一次抽奖机会,每次抽奖的奖金及对应的概率分别为:
奖金 | 50 | 100 |
概率 |
|
|
现在从不低于90同学中随机选一名同学,记其获奖金额为![]() ,以样本估计总体,将频率视为概率,求
,以样本估计总体,将频率视为概率,求![]() 的分布列和数学期望.
的分布列和数学期望.
(参考数据:![]() )
)