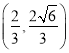题目内容
【题目】已知过抛物线y2＝4x焦点F的直线l交抛物线于A、B两点（点A在第一象限），若
3
，则直线l的斜率为（ ）
A.2B.
C.
D.
【答案】D
【解析】
作出抛物线的准线，设A、B在l上的射影分别是C、D，连接AC、BD，过B作BE⊥AC于E.由抛物线的定义结合题中的数据，可算出Rt△ABE中，cos∠BAE
，得∠BAE＝60°，即直线AB的倾斜角为60°，从而得到直线AB的斜率k值.
作出抛物线的准线l：x＝﹣1，设A、B在l上的射影分别是C、D，
连接AC、BD，过B作BE⊥AC于E.
∵
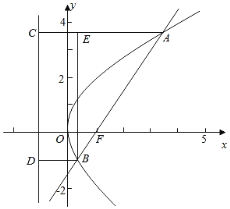
3
，∴设AF＝3m，BF＝m，
由点A、B分别在抛物线上，结合抛物线的定义，得AC＝3m，BD＝m.
因此，Rt△ABE中，cos∠BAE，得∠BAE＝60°
所以，直线AB的倾斜角∠AFx＝60°，
得直线AB的斜率k＝tan60°
，
故选：D.
练习册系列答案
相关题目
