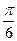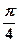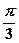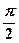题目内容
如图一,平面四边形 关于直线
关于直线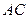 对称,
对称,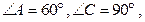
 .
.
把 沿
沿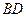 折起(如图二),使二面角
折起(如图二),使二面角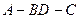 的余弦值等于
的余弦值等于 .对于图二,
.对于图二,
(Ⅰ)求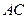 ;
;
(Ⅱ)证明: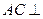 平面
平面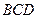 ;
;
(Ⅲ)求直线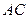 与平面
与平面 所成角的正弦值.
所成角的正弦值.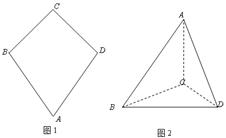
 关于直线
关于直线 对称,
对称,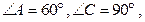
 .
.把
 沿
沿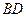 折起(如图二),使二面角
折起(如图二),使二面角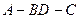 的余弦值等于
的余弦值等于 .对于图二,
.对于图二,(Ⅰ)求
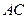 ;
;(Ⅱ)证明:
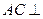 平面
平面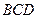 ;
;(Ⅲ)求直线
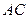 与平面
与平面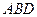 所成角的正弦值.
所成角的正弦值.
(1)

(2)略
(3)

解:(Ⅰ)取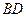 的中点
的中点 ,连接
,连接 ,
,
由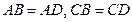 ,得:
,得: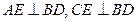
 就是二面角
就是二面角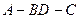 的平面角,
的平面角, ……………………2分
……………………2分
在 中
中 ,
,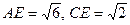
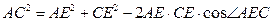
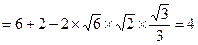
 ………………………………………4分
………………………………………4分
(Ⅱ)由 ,
,

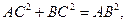


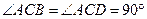
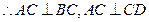 , 又
, 又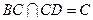
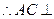 平面
平面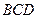 .………………8分
.………………8分
(Ⅲ)方法一:由(Ⅰ)知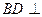 平面
平面
 平面
平面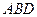
∴平面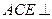 平面
平面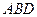 平面
平面 平面
平面 ,
,
作 交
交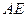 于
于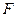 ,则
,则 平面
平面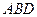 ,
,
 就是
就是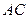 与平面
与平面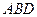 所成的角
所成的角 .……12分
.……12分
方法二:设点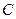 到平面
到平面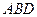 的距离为
的距离为 ,
,
∵

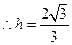 于是
于是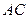 与平面
与平面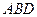 所成角
所成角 的正弦为
的正弦为  .
.
方法三:以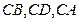 所在直线分别为
所在直线分别为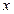 轴,
轴,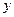 轴和
轴和 轴建立空间直角坐标系
轴建立空间直角坐标系 ,
,
则 .
.
设平面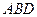 的法向量为
的法向量为
 ,则
,则

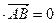 ,
, 
 ,
,

取 ,则
,则
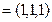 , 于是
, 于是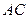 与平面
与平面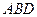 所成角
所成角 的正弦即
的正弦即
 .
.
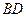 的中点
的中点 ,连接
,连接 ,
,由
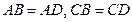 ,得:
,得: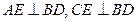
 就是二面角
就是二面角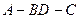 的平面角,
的平面角, ……………………2分
……………………2分在
 中
中 ,
,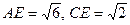
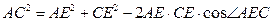
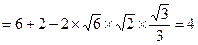
 ………………………………………4分
………………………………………4分 (Ⅱ)由
 ,
,

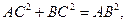


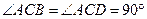
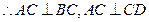 , 又
, 又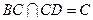
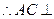 平面
平面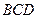 .………………8分
.………………8分(Ⅲ)方法一:由(Ⅰ)知
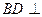 平面
平面
 平面
平面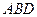
∴平面
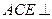 平面
平面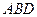 平面
平面 平面
平面 ,
,作
 交
交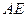 于
于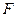 ,则
,则 平面
平面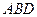 ,
, 就是
就是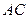 与平面
与平面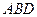 所成的角
所成的角 .……12分
.……12分方法二:设点
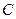 到平面
到平面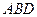 的距离为
的距离为 ,
,∵


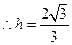 于是
于是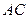 与平面
与平面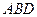 所成角
所成角 的正弦为
的正弦为  .
.方法三:以
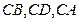 所在直线分别为
所在直线分别为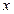 轴,
轴,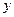 轴和
轴和 轴建立空间直角坐标系
轴建立空间直角坐标系 ,
, 则
 .
. 设平面
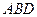 的法向量为
的法向量为
 ,则
,则
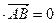 ,
, 
 ,
,

取
 ,则
,则
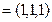 , 于是
, 于是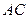 与平面
与平面 所成角
所成角 的正弦即
的正弦即 .
.
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
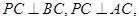 点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。
点E,F,G分别是所在棱的中点,则下面结论中正确的是: 。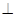 平面ABC
平面ABC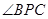 是直线EF与直线PC所成的角
是直线EF与直线PC所成的角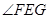 是平面PAB与平面ABC所成二面角的平面角
是平面PAB与平面ABC所成二面角的平面角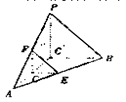
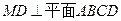 ,
,  ,且MD=NB=1,E为BC的中点
,且MD=NB=1,E为BC的中点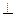 平面AMN?若存在,求线段AS的长;若不存在,请说明理由
平面AMN?若存在,求线段AS的长;若不存在,请说明理由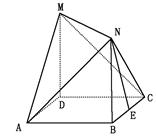

 中,棱长为
中,棱长为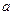
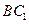 与
与 所成的角;
所成的角;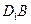 与平面
与平面 所成角的正切值;
所成角的正切值;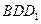
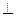 平面
平面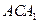 .
.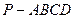 中,
中, 底面
底面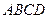 ,
,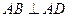 ,
,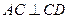 ,
,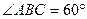 ,
,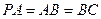 ,
,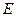 是
是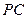 的中点.
的中点.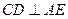 ;
;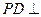 面
面 ;
;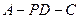 的平面角的正弦值.
的平面角的正弦值.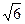 的等边三角形,另外两个面是等腰直角三角形,则这个三棱锥的体积为
的等边三角形,另外两个面是等腰直角三角形,则这个三棱锥的体积为 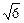 ④AC垂直于截面BDE
④AC垂直于截面BDE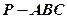 中,
中,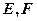 分别是棱
分别是棱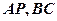 的中点,
的中点,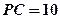 ,
,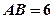 ,
,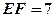 ,则异面直线
,则异面直线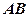 与
与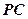 所成的角为 ( )
所成的角为 ( )