题目内容
【题目】已知椭圆![]()
![]() 的左右焦点分别为
的左右焦点分别为![]() ,直线
,直线![]() 经过椭圆的右焦点与椭圆交于
经过椭圆的右焦点与椭圆交于![]() 两点,且
两点,且![]() .
.
(I)求直线![]() 的方程;
的方程;
(II)已知过右焦点![]() 的动直线
的动直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 不同两点,是否存在
不同两点,是否存在![]() 轴上一定点
轴上一定点![]() ,使
,使![]() ?(
?(![]() 为坐标原点)若存在,求出点
为坐标原点)若存在,求出点![]() 的坐标;若不存在说明理由.
的坐标;若不存在说明理由.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]()
【解析】
(I)解法一:直线方程与椭圆方程联立化为一元二次方程,利用弦长公式即可得出.解法二:利用焦半径公式可得.
(II) II)设l2的方程为![]() 与椭圆联立:
与椭圆联立:![]() .假设存在点T(t,0)符合要求,设P(x1,y1),Q(x2,y2).∠OTP=∠OTQ
.假设存在点T(t,0)符合要求,设P(x1,y1),Q(x2,y2).∠OTP=∠OTQ![]() ,再利用根与系数的关系即可得出.
,再利用根与系数的关系即可得出.
解:(I)设![]() 的方程为
的方程为![]() 与椭圆联立得
与椭圆联立得![]()
直线经过椭圆内一点,故![]() 恒成立,设
恒成立,设![]() ,则
,则![]() ,
,![]()
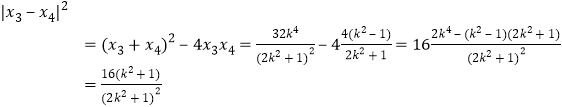 ,
,![]()
![]() 解得
解得![]() ,
,![]() 的方程为
的方程为![]() 或
或![]() ;
;
解2:由焦半径公式有![]() ,解得
,解得![]() .
.
(II)设![]() 的方程为
的方程为![]() 与椭圆联立:
与椭圆联立:![]() ,由于过椭圆内一点,
,由于过椭圆内一点,![]()
假设存在点![]() 符合要求,设
符合要求,设![]() ,韦达定理:
,韦达定理:![]()
![]()
![]() ,点在直线
,点在直线![]() 上有
上有
![]() ,即
,即![]() ,
,![]()
![]() ,
,
解得![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程![]() ;
;
(3)试预测加工10个零件需要多少时间.
参考公式:回归直线![]() ,
,
其中 ,
,![]()
