题目内容
【题目】已知数列{an}的前n项和为Sn ， 若a1=1，且Sn=tan﹣ 
，其中n∈N*．
（1）求实数t的值和数列{an}的通项公式；
（2）若数列{bn}满足bn=log3a2n ， 求数列{ 
}的前n项和Tn ．
【答案】
（1）解：当n=1时，a1=S1=ta1﹣ 
，由a1=1，即1=t﹣ ，
解得：t= 
，
∴Sn= an﹣ ，
当n≥2时，Sn﹣1= an﹣1﹣ ，
∴an=Sn﹣Sn﹣1=（ an﹣ ）﹣（ an﹣1﹣ ），即an=3an﹣1，
∴数列{an}是以1为首项，以3为公比的等比数列，
∴an=a1qn﹣1=3n﹣1，
当n=1时，an=3n﹣1，成立，
∴数列{an}的通项公式an=3n﹣1
（2）解：由（1）可知：bn=log3a2n=log332n﹣1=2n﹣1，
= 
= （ 
﹣ 
），
数列{ }的前n项和Tn，Tn= （1﹣ 
）+ （ ﹣ 
）+…+ （ ﹣ ），
= （1﹣ + ﹣ +…+ ﹣ ），
= （1﹣ ），
= 
，
数列{ }的前n项和Tn=
【解析】（1）由当n=1时，a1=S1=ta1﹣ ，由a1=1，即1=t﹣ ，即可求得t的值，Sn= an﹣ ，当n≥2时，Sn﹣1= an﹣1﹣ ，an=Sn﹣Sn﹣1 ， 整理得：an=3an﹣1 ， 数列{an}是以1为首项，以3为公比的等比数列，根据等比数列的通项公式求得数列{an}的通项公式；（2）由（1）可知：bn=log3a2n=log332n﹣1=2n﹣1， = = （ ﹣ 
），利用“裂项法”即可求得数列{ }的前n项和Tn ．
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系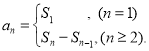
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式才能正确解答此题．
能力评价系列答案
唐印文化课时测评系列答案
【题目】某中学准备在开学时举行一次高三年级优秀学生座谈会，拟请20名来自本校高三(1)(2)(3)(4)班的学生参加，各班邀请的学生数如下表所示；
班级 | 高三（1） | 高三（2） | 高三（3） | 高三（4） |
人数 | 4 | 6 | 4 | 6 |
(1)从这20名学生中随机选出3名学生发言，求这3名学生中任意两个均不属于同一班级的概率；
(2)从这20名学生中随机选出3 名学生发言，设来自高三（3）的学生数为
，求随机变量的概率分布列和数学期望.
