题目内容
某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近视地表示为 ,已知此生产线的年产量最大为210吨.
,已知此生产线的年产量最大为210吨.
(Ⅰ) 求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(Ⅱ)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
 ,已知此生产线的年产量最大为210吨.
,已知此生产线的年产量最大为210吨.(Ⅰ) 求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(Ⅱ)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
(Ⅰ)年产量为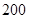 吨时,生产每吨产品的平均成本最低,最低成本为
吨时,生产每吨产品的平均成本最低,最低成本为 万元;(Ⅱ)当年产量为
万元;(Ⅱ)当年产量为 吨时,可以获得最大利润,最大利润是
吨时,可以获得最大利润,最大利润是 万元.
万元.
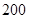 吨时,生产每吨产品的平均成本最低,最低成本为
吨时,生产每吨产品的平均成本最低,最低成本为 万元;(Ⅱ)当年产量为
万元;(Ⅱ)当年产量为 吨时,可以获得最大利润,最大利润是
吨时,可以获得最大利润,最大利润是 万元.
万元.试题分析:(Ⅰ)先根据定义将平均成本的表达式求出来,然后利用基本不等式求平均成本的最小值,但需注意基本不等式适用时的三个基本条件;(Ⅱ)先将总利润的函数解析式求出来,然后利用函数的单调性与最值的相关方法求总利润的最大值.
试题解析:(Ⅰ)每吨产品的平均成本

当且仅当
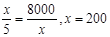 取等号即x=200<210 满足。
取等号即x=200<210 满足。年产量为200吨时,生产每吨产品的平均成本最低,最低成本为32万元; 5分
(Ⅱ)设总利润为
 万元,
万元,则

 在
在 上是增函数
上是增函数 时,
时, 有最大值为
有最大值为
 年产量为210吨时,可以获得最大利润1660万元. 10分
年产量为210吨时,可以获得最大利润1660万元. 10分
练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
 满足
满足 ,则
,则 的最大值是 .
的最大值是 . 满足约束条件.
满足约束条件. 若目标函数
若目标函数 的最大值为1,则
的最大值为1,则 的最小值为 .
的最小值为 . 满足
满足 ,则
,则 的最大值是
的最大值是  ,
, ,且
,且 ,那么
,那么 的取值范围是( )
的取值范围是( )
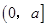


 的最大值为( )
的最大值为( )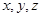 满足
满足 ,则当
,则当 取得最大值时,
取得最大值时, 的最大值为( )
的最大值为( )







 ,
, 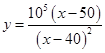 ,则当
,则当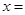 时,
时, 取最大值,最大值为 .
取最大值,最大值为 .