Question

【题目】记 表示正整数 在十进制下的各位数码之和.定义，证明：对任意的 ，存在无穷多个，，使得 .

Answer 1

【答案】见解析

【解析】

先证明两个引理．

引理1 设，有 .

引理1的证明 对任意，有.

设，.

反复利用式①得

.

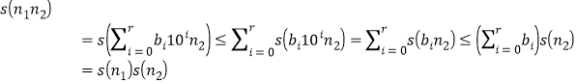引理2 对任意，存在， ，满足，，.

引理2的证明 取 ，则，.

由三进制表示的唯一性，知当（可重集合）时， .

于是，的每一位上的数码最大为2.故，.

类似于前面的讨论，中的每一位上的数字最大为6.从而，.

引理1、2得证．

下面用反证法证明原题.

假设只有有限个正整数 满足条件.则存在一个，使得当 时， .

设.则，，.

依次下去，知对任意，均有.

再取一个充分大的，使得 ，且 .

由引理2 ，知存在，满足，，.

故由引理1知.

但，矛盾.

从而，对任意，存在无穷多个， ，使得.