题目内容
【题目】记函数![]() 的定义域为A,
的定义域为A,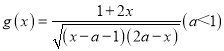 的定义域为B.
的定义域为B.
(1)求A;
(2)若BA,求实数a的取值范围.
【答案】(1)(-∞,-1)∪[1,+∞)(2)(-∞,-2]∪[![]() ,1)
,1)
【解析】
(1)由根式内部的代数式大于等于0求解分式不等式可得A;
(2)由分母中根式内部的代数式大于0求解B,再由集合间的包含关系列式求得实数a的取值范围.
解:(1)由2-![]() ≥0,得
≥0,得![]() ≥0,
≥0,
即x<-1或x≥1.
即A=(-∞,-1)∪[1,+∞);
(2)由(x-a-1)(2a-x)>0,得(x-a-1)(x-2a)<0.
∵a<1,∴a+1>2a,则B=(2a,a+1).
∵BA,∴2a≥1或a+1≤-1,即a≥![]() 或a≤-2,而a<1,
或a≤-2,而a<1,
∴![]() ≤a<1或a≤-2,
≤a<1或a≤-2,
故当BA时,实数a的取值范围是(-∞,-2]∪[![]() ,1).
,1).

练习册系列答案
相关题目