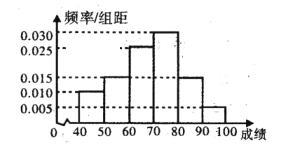
题目内容
【题目】将正整数1，2，…，10填于正五角星的十个顶点处，使得每条直线上所填四个数之和相等，问：这种填数方案是否存在?若存在，请给出填数方案的个数（经过旋转或对称之后能重合的方案视为同一种方案）；若不存在，请说明理由．
【答案】见解析
【解析】
若存在满足要求的填数方案，则每条直线上的四个数之和为
．
如图，令五角星外顶点所填数分别为
，
，…，
，
对应的内顶点所填数分别为
，
，…，
．
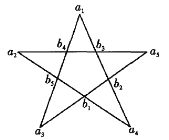
则
（
）此处下角标取模5非负剩余．
若
是一种填数方案，作互补变换
，则
也是一种不同的填数方案．
注意到，10必须与1、2均共线，9必须与1共线．
否则，10所在的两条直线上的数之和
，矛盾．
若1填在内顶点处，不妨设
，再由对称性，不妨设
．
由
，
，
，
知
，
，且
．
经验证，当
时，方案不存在．
若1填在外顶点处，不妨设
．
若10填在内顶点处，则作上述互补变换，便得到一个有1填在内顶点处的方案．
于是，10也填在外顶点处．
又
，于是
或
．
不妨假设，
，经验证，此时的填数方案也不存在．
综上，不存在满足要求的填数方案．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
