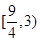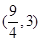题目内容
已知函数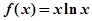 ,
,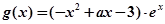 (其中
(其中 实数,
实数, 是自然对数的底数).
是自然对数的底数).
(Ⅰ)当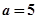 时,求函数
时,求函数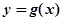 在点
在点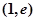 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间
在区间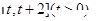 上的最小值;
上的最小值;
(Ⅲ) 若存在 ,使方程
,使方程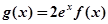 成立,求实数
成立,求实数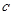 的取值范围.
的取值范围.
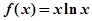 ,
,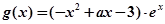 (其中
(其中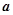 实数,
实数,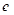 是自然对数的底数).
是自然对数的底数).(Ⅰ)当
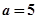 时,求函数
时,求函数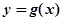 在点
在点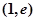 处的切线方程;
处的切线方程;(Ⅱ)求
 在区间
在区间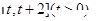 上的最小值;
上的最小值;(Ⅲ) 若存在
 ,使方程
,使方程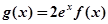 成立,求实数
成立,求实数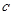 的取值范围.
的取值范围.(1) 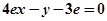
(2)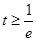 时,在区间
时,在区间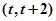 上,
上,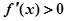 ,
,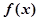 为增函数,所以
为增函数,所以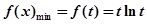
当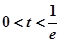 时,
时, 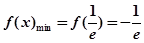
(3)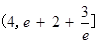
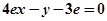
(2)
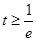 时,在区间
时,在区间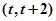 上,
上,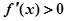 ,
,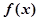 为增函数,所以
为增函数,所以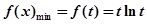
当
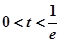 时,
时, 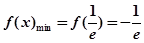
(3)
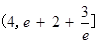
试题分析:解:(Ⅰ)当
 时
时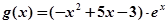 ,
,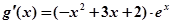 ┈┈1分
┈┈1分故切线的斜率为
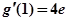 , ┈┈┈┈ 2分
, ┈┈┈┈ 2分所以切线方程为:
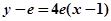 ,即
,即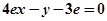 . ┈┈┈┈ 3分
. ┈┈┈┈ 3分(Ⅱ)
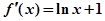 ,
,令
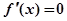 ,得
,得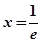 4分
4分①
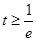 时,在区间
时,在区间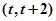 上,
上,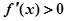 ,
,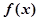 为增函数,
为增函数,所以
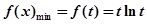 5分
5分②当
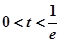 时,在区间
时,在区间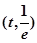 上
上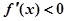 ,
,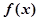 为减函数, 6分
为减函数, 6分在区间
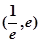 上
上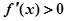 ,
,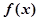 为增函数, 7分
为增函数, 7分所以
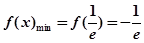 8分
8分(Ⅲ) 由
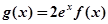 可得
可得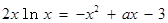
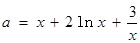 , 9分
, 9分令
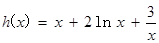 ,
,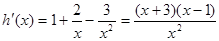 10分
10分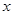 | 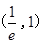 |  | 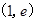 |
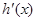 | 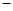 |  |  |
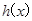 | 单调递减 | 极小值(最小值) | 单调递增 |
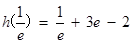 ,
,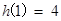 ,
,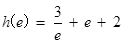
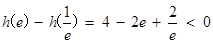 ┈┈┈┈ 13分
┈┈┈┈ 13分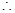 实数
实数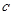 的取值范围为
的取值范围为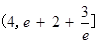 ┈┈┈┈ 14分
┈┈┈┈ 14分点评:解决的关键是对于导数的符号与函数单调性关系的运用,以及结合极值的概念得到最值,属于中档题

练习册系列答案
相关题目
 ,且
,且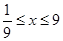 .
. 的值;
的值;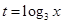 ,求
,求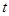 取值范围;
取值范围;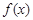 表示成以
表示成以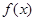 的最大值与最小值及与之对应的x的值.
的最大值与最小值及与之对应的x的值.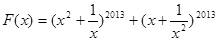 在区间
在区间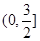 上的最小值为 .
上的最小值为 .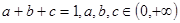 ,求证:
,求证: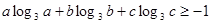 ;
;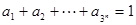 ,
,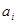 >0(i=1,2,3,…,3n),求证:
>0(i=1,2,3,…,3n),求证: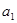
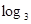
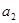
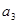
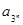
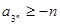
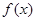 与
与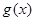 ,若区间
,若区间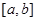 上
上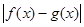 的最大值称为
的最大值称为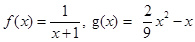 在
在 上的“绝对差”为
上的“绝对差”为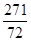
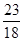
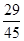
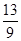
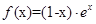 的单调递减区间 .
的单调递减区间 . 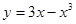 的单调递增区间是
的单调递增区间是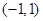
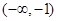
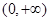
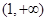
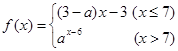 ,若数列
,若数列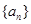 满足
满足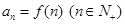 ,且对任意正整数
,且对任意正整数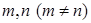 都有
都有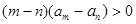 成立,则实数
成立,则实数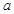 的取值范围是( )
的取值范围是( )