Question

【题目】已知数列{an}的前n项和为Sn，且满足an=2Sn﹣1（n∈N*） （Ⅰ）求证：数列{an}为等比数列；
（Ⅱ）若bn=（2n+1）an ， 求{bn}的前n项和Tn ．

Answer 1

【答案】证明：（Ⅰ）∵数列{an}的前n项和为Sn ， 且满足an=2Sn﹣1（n∈N*）， 当n=1时，a1=2S1﹣1=2a1﹣1，解得a1=1，
当n≥2时，由an=2Sn﹣1，①，得an﹣1=2Sn﹣1﹣1，②，
①﹣②，得：an﹣an﹣1=2an ， 整理，得an=﹣an﹣1 ，
∴{an}是首项为1，公比为﹣1的等比数列．
解：（Ⅱ）∵{an}是首项为1，公比为﹣1的等比数列，
∴ ，
∴bn=（2n+1）an=（2n+1）（﹣1）n﹣1 ，
∴{bn}的前n项和：
Tn=3（﹣1）0+5（﹣1）+7（﹣1）2+…+（2n+1）（﹣1）n﹣1 ， ①
﹣Tn=3（﹣1）+5（﹣1）2+7（﹣1）3+…+（2n+1）（﹣1）n ， ②
①﹣②，得：2Tn=3+2[（﹣1）+（﹣1）2+（﹣1）3+…+（﹣1）n﹣1]﹣（2n+1）（﹣1）n
=3+2× 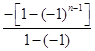﹣（2n﹣1）（﹣1）n
=（2n+2）（﹣1）n﹣1+2，
∴Tn=（n+1）（﹣1）n﹣1+1=1﹣（n+1）（﹣1）n
【解析】（Ⅰ）an=2Sn﹣1（n∈N*），推导出a1=1，an=﹣an﹣1 ， 由此能证明{an}是首项为1，公比为﹣1的等比数列．（Ⅱ）由 ，得bn=（2n+1）an=（2n+1）（﹣1）n﹣1 ， 由此利用错位相减法能求出{bn}的前n项和．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系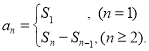，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．