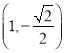Question

【题目】△ABC的内角A、B、C的对边分别为a、b、c．己知asinA+csinC﹣ asinC=bsinB， （Ⅰ）求B；
（Ⅱ）若A=75°，b=2，求a，c．

Answer 1

【答案】解：（Ⅰ）由正弦定理得a2+c2﹣ ac=b2 ， 由余弦定理可得b2=a2+c2﹣2accosB，
故cosB= ，B=45°
（Ⅱ）sinA=sin（30°+45°）=sin30°cos45°+cos30°sin45°=
故a=b× = =1+
∴c=b× =2× =
【解析】（Ⅰ）利用正弦定理把题设等式中的角的正弦转换成边的关系，代入余弦定理中求得cosB的值，进而求得B．（Ⅱ）利用两角和公式先求得sinA的值，进而利用正弦定理分别求得a和c．