题目内容
【题目】若![]() 是公差不为0的等差数列
是公差不为0的等差数列![]() 的前
的前![]() 项和,且
项和,且![]() 成等比数列,
成等比数列,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() 是数列
是数列![]() 的前
的前![]() 项和,求使得
项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数
都成立的最小正整数![]() .
.
【答案】(1) ![]() (2)
(2) ![]() 的最小值为
的最小值为![]() .
.
【解析】试题分析:第一问根据条件中数列为等差数列,设出等差数列的首项和公差,根据题中的条件,建立关于等差数列的首项和公差的等量关系式,从而求得结果,利用等差数列的通项公式求得数列的通项公式,第二问利用第一问的结果,先写出![]() ,利用裂项相消法求得数列
,利用裂项相消法求得数列![]() 的前
的前![]() 项和,根据条件,得出相应的不等式,转化为最值来处理,从而求得结果.
项和,根据条件,得出相应的不等式,转化为最值来处理,从而求得结果.
试题解析:(1)因为![]() 为等差数列,设
为等差数列,设![]() 的首项为
的首项为![]() ,公差为
,公差为![]()
![]() ,所以
,所以
![]() .又因为
.又因为![]() 成等比数列,所以
成等比数列,所以![]() .所以
.所以![]() .
.
因为公差![]() 不等于
不等于![]() ,所以
,所以![]() .又因为
.又因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(2)因为![]() ,
,
所以![]()
![]() .
.
要使![]() 对所有
对所有![]() 都成立,则有
都成立,则有![]() ,即
,即![]() .因为
.因为![]() ,所以
,所以![]() 的最小值为30.
的最小值为30.

练习册系列答案
相关题目
【题目】某种产品的广告费支出x(单位:万元)与销售额y(单位:万元)之间有如表对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
(1)求回归直线方程;
附:回归直线的斜率和截距的最小二乘估计公式分别为: 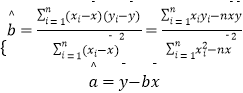 .
.
(2)试预测广告费支出为10万元时,销售额多大?