题目内容
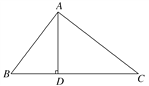
【题目】如图，在△ABC中，AD⊥BC于D，下列条件：
①∠B＋∠DAC＝90°，
②∠B＝∠DAC，
③
，
④AB2＝BD·BC.
其中一定能够判定△ABC是直角三角形的共有( )
A. 3个 B. 2个 C. 1个 D. 0个
【答案】A
【解析】
①不能.
∵AD⊥BC，∴∠B+∠BAD=90°.∵∠B+∠DAC=90°，∴∠BAD=∠DAC，
∴△ABD≌△ACD（ASA），∴AB=AC，∴△ABC是等腰三角形，
∴无法证明△ABC是直角三角形；
②能.
∵AD⊥BC，∴∠B+∠BAD=90°.
∵∠B=∠DAC，∴∠BAC=∠BAD+∠DAC=∠BAD+∠B=90°；
③能.∵CD：AD=AC：AB，∠ADB=∠CDA=90°，
∴Rt△ABD∽Rt△CAD，∴∠ABD=∠CAD，∠BAD=∠ACD.
∵∠ABD+∠BAD=90°，∴∠CAD+∠BAD=90°.∵∠BAC=∠CAD+∠BAD，
∴∠BAC=90°；
④能.
∵能说明△CBA∽△ABD，又∵△ABD是直角三角形，∴△ABC一定是直角三角形.
故选A.
金博士一点全通系列答案
【题目】某花店每天以每枝
元的价格从农场购进若干枝玫瑰花，然后以每枝
元的价格出售.如果当天卖不完，剩下的玫瑰花做垃圾处理.
（1）若花店一天购进
枝玫瑰花，求当天的利润
（单位：元）关于当天需求量
（单位：枝， 
）的函数解析式.
（2）花店记录了
天玫瑰花的日需求量（单位：枝），整理得下表：
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
假设花店在这
天内每天购进
枝玫瑰花，求这
天的日利润（单位：元）的平均数.
【题目】对某电子元件进行寿命追踪调查，情况如下．
寿命（h） | 100～200 | 200～300 | 300～400 | 400～500 | 500～600 |
个 数 | 20 | 30 | 80 | 40 | 30 |
（1）列出频率分布表；
（2）画出频率分布直方图；
（3）估计元件寿命在100～400h以内的在总体中占的比例．
