题目内容
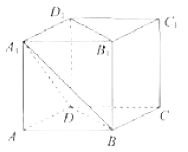
【题目】如图，在正方体
中， 
，平面
经过
，直线
，则平面
截该正方体所得截面的面积为（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】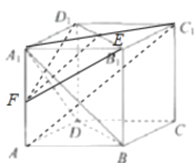
如图所示，连接
与
交于
，取
的中点
，连接
，则
， 
平面
平面
平面
， 
是满足条件的截面，由正方体的性质可得
， 
平面
截该正方体所得截面的面积为
，故选D.
【方法点晴】本题主要考查线面平行的判定定理棱锥的体积公式，属于难题.证明线面平行的常用方法：①利用线面平行的判定定理，使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线，可利用几何体的特征，合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质，即两平面平行，在其中一平面内的直线平行于另一平面.
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
【题目】某花店每天以每枝
元的价格从农场购进若干枝玫瑰花，然后以每枝
元的价格出售.如果当天卖不完，剩下的玫瑰花做垃圾处理.
（1）若花店一天购进
枝玫瑰花，求当天的利润
（单位：元）关于当天需求量
（单位：枝， 
）的函数解析式.
（2）花店记录了
天玫瑰花的日需求量（单位：枝），整理得下表：
日需求量 |
|
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
|
假设花店在这
天内每天购进
枝玫瑰花，求这
天的日利润（单位：元）的平均数.
【题目】某种产品的广告费支出x（单位：万元）与销售额y（单位：万元）之间有如表对应数据：
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
（1）求回归直线方程；
附：回归直线的斜率和截距的最小二乘估计公式分别为：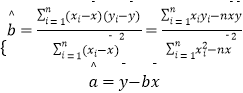 
．
（2）试预测广告费支出为10万元时，销售额多大？