题目内容
【题目】已知函数f(x)=a(2cos2 ![]() +sinx)+b
+sinx)+b
(1)若a=﹣1,求f(x)的单调增区间;
(2)若x∈[0,π]时,f(x)的值域是[5,8],求a,b的值.
【答案】
(1)解:f(x)=a(1+cosx+sinx)+b= ![]() asin(x+
asin(x+ ![]() )+a+b,
)+a+b,
当a=﹣1时,由2kπ+ ![]() ≤x+
≤x+ ![]() ≤2kπ+
≤2kπ+ ![]() π,得2kπ+
π,得2kπ+ ![]() ≤x≤2kπ+
≤x≤2kπ+ ![]() π,
π,
∴f(x)的单调增区间为[2kπ+ ![]() ,2kπ+
,2kπ+ ![]() π](k∈Z)
π](k∈Z)
(2)解:∵0≤x≤π,∴ ![]() ≤x+
≤x+ ![]() ≤
≤ ![]() π,
π,
∴﹣ ![]() ≤sin(x+
≤sin(x+ ![]() )≤1,依题意知a≠0,
)≤1,依题意知a≠0,
分两种情况考虑:
1°当a>0时, 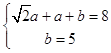 ,
,
∴a=3( ![]() ﹣1),b=5;
﹣1),b=5;
2°当a<0时,  ,
,
∴a=﹣3( ![]() ﹣1),b=8,
﹣1),b=8,
综上所述:a=3 ![]() ﹣3,b=5或a=3﹣3
﹣3,b=5或a=3﹣3 ![]() ,b=8
,b=8
【解析】函数f(x)解析式利用二倍角的余弦函数公式化简,整理后再利用两角和与差的正弦函数公式化为一个角的正弦函数,(1)将a=﹣1代入,利用正弦函数的递增区间即可确定出f(x)的递增区间;(2)根据x的范围求出这个角的范围,确定出正弦函数的值域,根据f(x)的值域,分a小于0与大于0两种情况考虑,分别列出关于a与b的方程组,求出方程组的解即可得到a与b的值.

练习册系列答案
相关题目
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)现有![]() 人前去该商场购物,求获得纪念品的数量
人前去该商场购物,求获得纪念品的数量![]() 的分布列与数学期望.
的分布列与数学期望.