Question

【题目】记max{m，n}= ，设F（x，y）=max{|x2+2y+2|，|y2﹣2x+2|}，其中x，y∈R，则F（x，y）的最小值是

Answer 1

【答案】1
【解析】解：∵|x2+2y+2|=|（x﹣1）2+2（x+y）+1|，|y2﹣2x+2|=|（y+1）2﹣2（x+y）+1|，
若x+y＞0，则|（x﹣1）2+2（x+y）+1|＞1，
则F（x，y）＞1，
若x+y＜0，则|（y+1）2﹣2（x+y）+1|＞1，
则F（x，y）＞1；
而当 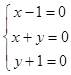，即x=1，y=﹣1时，
F（x，y）=1，
故F（x，y）的最小值是1．
所以答案是：1．
【考点精析】关于本题考查的函数的最值及其几何意义，需要了解利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能得出正确答案．