Question

【题目】已知直线l1过点A（﹣1，0），且斜率为k，直线l2过点B（1，0），且斜率为﹣2k，其中k≠0，又直线l1与l2交于点M．
（1）求动点M的轨迹方程；
（2）若过点N（ ，1）的直线l交动点M的轨迹于C、D两点，且N为线段CD的中点，求直线l的方程．

Answer 1

【答案】
（1）解：设M（x，y），

∵直线l1与l2交于点M，

∴联立得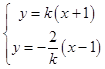： （k≠0），

消去k得： =﹣2，

则动点M的轨迹方程为2x2+y2=2（x≠±1）

（2）解：由（1）得M的轨迹方程为2x2+y2=2（x≠±1），

设点C（x1，y1），D（x2，y2），则有2x12+y12=2①，2x22+y22=2②，

①﹣②得：2（x1﹣x2）（x1+x2）+（y1﹣y2）（y1+y2）=0，即 =﹣2× ，

∵N（ ，1）为CD的中点，

∴x1+x2=1，y1+y2=2，

∴直线l的斜率k=﹣1，

∴直线l的方程为y﹣1=﹣（x﹣ ），即2x+2y﹣3=0

【解析】（1）设M坐标为（x，y），表示出两直线方程，联立消去k即可确定出M的轨迹方程；（2）设出C与D坐标，分别代入M的轨迹方程，整理由根据N为CD中点，求出直线l斜率，即可确定出直线l方程．