题目内容
设等差数列{an}的前n项和为Sn，Sm-1=-2，Sm=0，Sm+1=3，则正整数m的值为______．
由题意可得am=Sm-Sm-1=0-（-2）=2，
am+1=Sm+1-Sm=3-0=3，
∴等差数列{an}的公差d=am+1-am=3-2=1，
由通项公式可得am=a1+（m-1）d，
代入数据可得2=a1+m-1，①
再由求和公式可得Sm=ma1+
d，
代入数据可得0=ma1+
，②
联立①②可解得m=5
故答案为：5
am+1=Sm+1-Sm=3-0=3，
∴等差数列{an}的公差d=am+1-am=3-2=1，
由通项公式可得am=a1+（m-1）d，
代入数据可得2=a1+m-1，①
再由求和公式可得Sm=ma1+
| m(m-1) |
| 2 |
代入数据可得0=ma1+
| m(m-1) |
| 2 |
联立①②可解得m=5
故答案为：5
练习册系列答案
相关题目
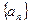中，
，
。
；
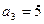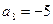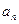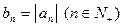，求数列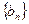
的前20项和
。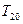