题目内容
在等差数列{an}中,a3+a5+a7+a9+a11=20,则a1+a13=______.
由等差数列的性质可得
a3+a5+a7+a9+a11=(a3+a11)+a7+(a5+a9)
=2a7+a7+2a7=5a7=20
∴a7=4
∴a1+a13=2a7=8
故答案为:8
a3+a5+a7+a9+a11=(a3+a11)+a7+(a5+a9)
=2a7+a7+2a7=5a7=20
∴a7=4
∴a1+a13=2a7=8
故答案为:8

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
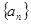 中,已知
中,已知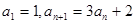 ,则
,则