题目内容
等差数列{an}中，a1+a4+a7=15，a2a4a6=45，求数列的通项公式．
∵等差数列{an}中，a1+a4+a7=15=3a4，a2a4a6=45，
∴a4=5，∴
，解得①
，或②
．
由①求得公差d=2，通项公式为an=a2+（n-2）d=2n-3；
由②公差d=-2，通项公式为an=a2+（n-2）d=5-2n．
综上可得，通项公式为an=2n-3，或 an=5-2n．
∴a4=5，∴
|
|
|
由①求得公差d=2，通项公式为an=a2+（n-2）d=2n-3；
由②公差d=-2，通项公式为an=a2+（n-2）d=5-2n．
综上可得，通项公式为an=2n-3，或 an=5-2n．
练习册系列答案
相关题目
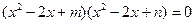的四个根组成一个首项为
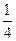的等差数列，
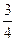C.
