题目内容
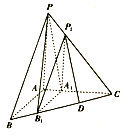
【题目】如图,在三棱锥![]() 中,
中,![]() 两两垂直,
两两垂直,![]() ,平面
,平面![]() 平面
平面![]() ,且
,且![]() 与棱
与棱![]() 分别交于
分别交于![]() 三点.
三点.
(1)过![]() 作直线
作直线![]() ,使得
,使得![]() ,
,![]() ,请写出作法并加以证明;
,请写出作法并加以证明;
(2)若α将三梭锥P﹣ABC分成体积之比为8:19的两部分(其中,四面体P1A1B1C的体积更小),D为线段B1tC的中点,求直线P1D与平面PA1B1所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】分析:(1)取BC的中点H,连结AH,则直线AH即为要求的直线l;
(2)根据体积比得出P1A1=A1B1=2,将四棱锥分解成两个小三棱锥计算体积.
详解:(1)作法:取![]() 的中点
的中点![]() ,连接
,连接![]() ,则直线
,则直线![]() 即为要求作的直线
即为要求作的直线![]() .
.
证明如下:∵![]() ,
,![]() ,且
,且![]() ,∴
,∴![]() 平面
平面![]() .
.
∵平面![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() .
.
又![]() ,
,![]() 为
为![]() 的中点,则
的中点,则![]() ,从而直线
,从而直线![]() 即为要求作的直线
即为要求作的直线![]() .
.
(2)∵![]() 将三棱锥
将三棱锥![]() 分成体积之比为
分成体积之比为![]() 的两部分,
的两部分,
∴四面体![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积之比为
的体积之比为![]() ,
,
又平面![]() 平面
平面![]() ,∴
,∴![]() .
.
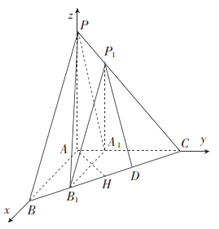
以![]() 为坐标原点,建立如图所示的空间直角坐标系
为坐标原点,建立如图所示的空间直角坐标系![]() ,设
,设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则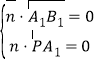 ,即
,即![]() ,
,
令![]() ,得
,得![]() .
.
则![]() .
.
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目