题目内容
已知梯形ABCD中,AB=DC=AD,AC和BD是它的对角线.用三段论证明:AC平分∠BCD,BD平分∠CBA.
证明略
证明 (1)两平行线与第三直线相交,内错角相等(大前提)
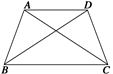
∠BCA与∠CAD是平行线AD,BC被AC所截内错角(小前提)
所以,∠BCA=∠CAD(结论)
(2)等腰三角形两底角相等(大前提)
△CAD是等腰三角形,DA=DC(小前提)
所以,∠DCA=∠CAD(结论)
(3)等于同一个量的两个量相等(大前提)
∠BCA与∠DCA都等于∠CAD(小前提)
所以,∠BCA=∠DCA(结论)
(4)同理,BD平分∠CBA.

∠BCA与∠CAD是平行线AD,BC被AC所截内错角(小前提)
所以,∠BCA=∠CAD(结论)
(2)等腰三角形两底角相等(大前提)
△CAD是等腰三角形,DA=DC(小前提)
所以,∠DCA=∠CAD(结论)
(3)等于同一个量的两个量相等(大前提)
∠BCA与∠DCA都等于∠CAD(小前提)
所以,∠BCA=∠DCA(结论)
(4)同理,BD平分∠CBA.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
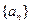 中,
中,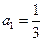 ,且前n项的算术平均数等于第n项的2n-1倍(
,且前n项的算术平均数等于第n项的2n-1倍(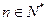 )。
)。 中,
中, ,若
,若 ,则
,则 ;若类比该命题,如图(2),三棱锥
;若类比该命题,如图(2),三棱锥 中,
中, 面
面 点在三角形
点在三角形 所在平面内的射影为
所在平面内的射影为 ,则有什么结论?命题是否是真命题.
,则有什么结论?命题是否是真命题.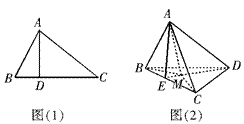
 的前
的前 项和为
项和为 ,则
,则 ,
, ,
, ,
, 成等差数列.类比
成等差数列.类比 的前
的前 ,则
,则 , ,
, , 成等比数列.
成等比数列.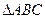 内一点,
内一点,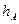 、
、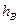 、
、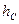 ,P到三边的距离依次为
,P到三边的距离依次为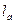 、
、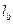 、
、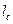 ,则有
,则有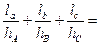 ______________;类比到空间,设P是四面体ABCD内一点,四顶点到对面的距离分别是
______________;类比到空间,设P是四面体ABCD内一点,四顶点到对面的距离分别是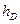 ,P到这四个面的距离依次是
,P到这四个面的距离依次是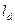 ,则有_________________。
,则有_________________。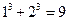 ; ⑵
; ⑵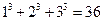 ;⑵
;⑵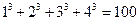 ,
, .
. 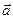 的性质
的性质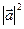 =
=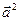 类比得到复数
类比得到复数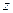 的性质
的性质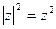 ;
; ,其中
,其中 为常数,等号右边的运算是通常意义的加乘运算,现已知
为常数,等号右边的运算是通常意义的加乘运算,现已知 ,
, ,且有一个非零实数m,使得对任意实数x,都有
,且有一个非零实数m,使得对任意实数x,都有 ,则
,则 ______________。
______________。