题目内容
10.已知x∈[0,π],则函数y=$\sqrt{3}$sinx-cosx的值域为( )| A. | [-2,2] | B. | [-1,2] | C. | [-1,1] | D. | [0,2] |
分析 根据两角和与差的正弦公式可得:y=2sin(x-$\frac{π}{6}$),再根据题意可得x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],然后利用正弦函数的图象可得-$\frac{1}{2}$≤sin(x-$\frac{π}{6}$)≤1,进而得解.
解答 解:由题意可得:y=$\sqrt{3}$sinx-cosx=2sin(x-$\frac{π}{6}$),
因为x∈[0,π],
所以x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
所以-$\frac{1}{2}$≤sin(x-$\frac{π}{6}$)≤1,
所以:-1≤y≤2.
故选:B.
点评 本题主要考查了正弦函数的有关性质,即值域与定义域.解题的关键是利用两角和与差的正弦余弦该点对函数解析式进行正确化简,以及对正弦函数的性质的熟练运用,属于基础题.

练习册系列答案
相关题目
18.定义在R上的函数f(x)满足:f′(x)>1-f(x),f(0)=3,f′(x)是f(x)的导函数,则不等式exf(x)>ex+2(其中e为自然对数的底数)的解集为( )
| A. | {x|x>0} | B. | {x|x<0} | C. | {x|x<-1或x>1} | D. | {x|x<-1或0<x<1} |
2.设随机变量ξ服从正态分布N(2,σ2),若P(ξ>4)=0.1,则P(ξ<0)=( )
| A. | 0.4 | B. | 0.2 | C. | 0.1 | D. | 0.05 |
19.利用二分法求方程2x+2x-7=0在区间(1,3)内近似解的过程中取区间的中点2,则下一个有该方程实根的区间是( )
| A. | (1,2) | B. | (2,3) | C. | (1,2)或(2,3) | D. | 不能确定 |

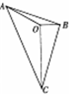 如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.
如图,已知O是△ABC内一点,∠AOB=150°,∠AOC=120°,向量$\overrightarrow{OA},\overrightarrow{OB}$,$\overrightarrow{OC}$的模分别为2,1,3,若$\overrightarrow{OC}$=m$\overrightarrow{OA}+n\overrightarrow{OB}$,则实数m+n的值为$-3-3\sqrt{3}$.