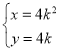题目内容
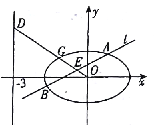
【题目】已知椭圆![]() 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 另一个焦点是
另一个焦点是![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 的内切圆面积的最大值.
的内切圆面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用将![]() 点的横坐标
点的横坐标![]() 代入直线
代入直线![]() ,求得
,求得![]() 点的坐标,代入
点的坐标,代入![]() 的坐标运算,求得
的坐标运算,求得![]() 的值,也即求得
的值,也即求得![]() 点的坐标,将
点的坐标,将![]() 的坐标代入椭圆,结合
的坐标代入椭圆,结合![]() ,解方程组求得
,解方程组求得![]() 的值,进而求得椭圆方程.(2)设出直线
的值,进而求得椭圆方程.(2)设出直线![]() 的方程,联立直线的方程和椭圆的方程并写出根与系数关系,由此求得
的方程,联立直线的方程和椭圆的方程并写出根与系数关系,由此求得![]() 的面积,利用导数求得面积的最大值,并由三角形与内切圆有关的面积公式,求得内切圆的半径的最大值.
的面积,利用导数求得面积的最大值,并由三角形与内切圆有关的面积公式,求得内切圆的半径的最大值.
(1)设椭圆方程为![]() ,点
,点![]() 在直线
在直线![]() 上,且点
上,且点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,则点
,则点![]() .
.
∵![]()
∴![]()
又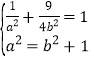
解得![]()
∴椭圆方程为![]()
(2)由(1)知,![]() ,过点
,过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,
两点,
则![]() 的周长为
的周长为![]() ,又
,又![]() (
(![]() 为三角形内切圆半径),
为三角形内切圆半径),
∴当![]() 的面积最大时,其内切圆面积最大.
的面积最大时,其内切圆面积最大.
设直线![]() 的方程为:
的方程为:![]() ,
,![]() ,则
,则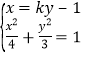
消去![]() 得
得![]() ,
,
∴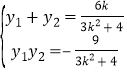
∴![]()
令![]() ,则
,则![]() ,∴
,∴![]()
令![]() ,
,![]()
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() ,当
,当![]() 时取等号,
时取等号,
即当![]() 时,
时,![]() 的面积最大值为3,
的面积最大值为3,
结合![]() ,得
,得![]() 的最大值为
的最大值为![]() ,
,
∴内切圆面积的最大值为![]() .
.

【题目】从某电子商务平台随机抽取了1000位网上购物者(年消费都达到2000元),并对他们的年龄进行了调查,统计情况如下表所示:
年龄 |
|
|
|
|
|
|
人数 | 100 | 150 | 400 | 200 | 100 | 50 |
该电子商务平台将年龄在![]() 的人群定义为消费主力军,其它年龄段定义为消费潜力军.
的人群定义为消费主力军,其它年龄段定义为消费潜力军.
(1)若该电子商务平台共10万位网上购物者,试估计消费主力军的人数;
(2)为了鼓励消费潜力军消费,该平台决定对年消费达到2000元的购物者发放代金券,消费主力军每人发放100元,消费潜力军每人发放200元.现采用分层抽样(按消费主力军与消费潜力军分层)的方式从参与调查的1000位网上购物者中抽取10人,并在这10人中随机抽取3人进行回访,求这3人获得代金券总金额![]() (单位:元)的分布列及数学期望.
(单位:元)的分布列及数学期望.