Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņ‘ŕń≥īőĽÓ∂Į÷–£¨”–5√Ż–“‘ň÷ģ–«.’‚5√Ż–“‘ň÷ģ–«Ņ…ĽŮĶ√![]() °Ę
°Ę![]() ŃĹ÷÷ĹĪ∆∑÷–Ķń“Ľ÷÷£¨≤ĘĻś∂®£ļ√ŅłŲ»ňÕ®ĻżŇ◊÷ņ“Ľ√∂÷ Ķōĺýő™ĶńųĽ◊”ĺŲ∂®◊‘ľļ◊Ó÷’ĽŮĶ√ńń“Ľ÷÷ĹĪ∆∑£®ųĽ◊”ĶńŃýłŲ√ś…ŌĶńĶ„ ż∑÷Īūő™1Ķ„°Ę2Ķ„°Ę3Ķ„°Ę4Ķ„°Ę5Ķ„°Ę6Ķ„£©£¨Ň◊÷ņĶ„ ż–°”ŕ3ĶńĽŮĶ√
ŃĹ÷÷ĹĪ∆∑÷–Ķń“Ľ÷÷£¨≤ĘĻś∂®£ļ√ŅłŲ»ňÕ®ĻżŇ◊÷ņ“Ľ√∂÷ Ķōĺýő™ĶńųĽ◊”ĺŲ∂®◊‘ľļ◊Ó÷’ĽŮĶ√ńń“Ľ÷÷ĹĪ∆∑£®ųĽ◊”ĶńŃýłŲ√ś…ŌĶńĶ„ ż∑÷Īūő™1Ķ„°Ę2Ķ„°Ę3Ķ„°Ę4Ķ„°Ę5Ķ„°Ę6Ķ„£©£¨Ň◊÷ņĶ„ ż–°”ŕ3ĶńĽŮĶ√![]() ĹĪ∆∑£¨Ň◊÷ņĶ„ ż≤Ľ–°”ŕ3ĶńĽŮĶ√
ĹĪ∆∑£¨Ň◊÷ņĶ„ ż≤Ľ–°”ŕ3ĶńĽŮĶ√![]() ĹĪ∆∑.
ĹĪ∆∑.
£®1£©«ů’‚5√Ż–“‘ň÷ģ–«÷–ĽŮĶ√![]() ĹĪ∆∑Ķń»ň żīů”ŕĽŮĶ√
ĹĪ∆∑Ķń»ň żīů”ŕĽŮĶ√![]() ĹĪ∆∑Ķń»ň żĶńłŇ¬ £Ľ
ĹĪ∆∑Ķń»ň żĶńłŇ¬ £Ľ
£®2£©…Ť![]() °Ę
°Ę![]() ∑÷Īūő™ĽŮĶ√
∑÷Īūő™ĽŮĶ√![]() °Ę
°Ę![]() ŃĹ÷÷ĹĪ∆∑Ķń»ň ż£¨≤Ęľ«
ŃĹ÷÷ĹĪ∆∑Ķń»ň ż£¨≤Ęľ«![]() £¨«ůňśĽķĪšŃŅ
£¨«ůňśĽķĪšŃŅ![]() Ķń∑÷≤ľŃ–ľį ż—ß∆ŕÕŻ.
Ķń∑÷≤ľŃ–ľį ż—ß∆ŕÕŻ.
°ĺīūįł°Ņ£®1£©![]() £Ľ£®2£©
£Ľ£®2£©![]() £¨
£¨![]() Ķń∑÷≤ľŃ–ľŻĹ‚őŲ.
Ķń∑÷≤ľŃ–ľŻĹ‚őŲ.
°ĺĹ‚őŲ°Ņ
◊Ō»«ů≥Ų5√Ż–“‘ň÷ģ–«÷–£¨√Ņ»ňĽŮĶ√AĹĪ∆∑ĶńłŇ¬ ļÕBĹĪ∆∑ĶńłŇ¬ £ģ£®1£©ĽŮĶ√AĹĪ∆∑Ķń»ň żīů”ŕĽŮĶ√BĹĪ∆∑Ķń»ň ż£¨Ķ√ĶĹĽŮĶ√AĹĪ∆∑Ķń»ň żŅ…ń‹ő™3£¨4£¨5£¨ņŻ”√∂ņŃĘ÷ōłī ‘—ť«ůĶ√łŇ¬ £Ľ£®2£©”…¶ő£Ĺ|X©ĀY|£¨Ņ…Ķ√¶őĶńŅ…ń‹»°÷Ķő™1£¨3£¨5£¨Õ¨—ýņŻ”√∂ņŃĘ÷ōłī ‘—ť«ůĶ√łŇ¬ £¨»ĽļůŃ–≥Ų∆Ķ¬ ∑÷≤ľĪŪ£¨īķ»Ž∆ŕÕŻĻę Ĺ«ů∆ŕÕŻ£ģ
’‚5√Ż–“‘ň÷ģ–«÷–£¨√Ņ»ňĽŮĶ√![]() ĹĪ∆∑ĶńłŇ¬ ő™
ĹĪ∆∑ĶńłŇ¬ ő™![]() £¨
£¨![]() ĹĪ∆∑ĶńłŇ¬ ő™
ĹĪ∆∑ĶńłŇ¬ ő™![]() .
.
£®1£©“™ĽŮĶ√![]() ĹĪ∆∑Ķń»ň żīů”ŕĽŮĶ√
ĹĪ∆∑Ķń»ň żīů”ŕĽŮĶ√![]() ĹĪ∆∑Ķń»ň ż£¨‘Ú
ĹĪ∆∑Ķń»ň ż£¨‘Ú![]() ĹĪ∆∑Ķń»ň żŅ…ń‹ő™3£¨4£¨5£¨‘Ú
ĹĪ∆∑Ķń»ň żŅ…ń‹ő™3£¨4£¨5£¨‘Ú
ňý«ůłŇ¬ ő™![]() .
.
£®2£©![]() ĶńŅ…ń‹»°÷Ķő™1£¨3£¨5£¨«“
ĶńŅ…ń‹»°÷Ķő™1£¨3£¨5£¨«“![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
ňý“‘![]() Ķń∑÷≤ľŃ– «£ļ
Ķń∑÷≤ľŃ– «£ļ
| 1 | 3 | 5 |
|
|
|
|
Ļ ňśĽķĪšŃŅ![]() Ķń ż—ß∆ŕÕŻ
Ķń ż—ß∆ŕÕŻ![]() .
.

 łŖ÷–ĪōňĘŐ‚ŌĶŃ–īūįł
łŖ÷–ĪōňĘŐ‚ŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņń≥ĽķĻĻ∂‘ń≥ –Ļ§–ĹĹ◊≤„Ķń ’»Ž«ťŅŲ”Ž≥¨«įŌŻ∑—––ő™ĹÝ––Ķų≤ť£¨ňśĽķ≥ť≤ťŃň200»ň£¨ĹęňŻ√«Ķń‘¬ ’»Ž£®Ķ•őĽ£ļįŔ‘™£©∆Ķ ż∑÷≤ľľį≥¨«įŌŻ∑—Ķń»ŌÕ¨»ň ż’ŻņŪĶ√ĶĹ»ÁŌ¬ĪŪłŮ£ļ
‘¬ ’»Ž£®įŔ‘™£© |
|
|
|
|
|
|
∆Ķ ż | 20 | 40 | 60 | 40 | 20 | 20 |
»ŌÕ¨≥¨«įŌŻ∑—Ķń»ň ż | 8 | 16 | 28 | 21 | 13 | 16 |
£®1£©łý囓‘…ŌÕ≥ľ∆ żĺ›ŐÓ–īŌ¬√ś![]() Ń–Ń™ĪŪ£¨≤ĘĽōīū «∑Ů”–99%Ķńį—ő’»Ōő™ĶĪ‘¬ ’»Ž“‘8000‘™ő™∑÷ĹÁĶ„ Ī£¨ł√ –ĶńĻ§–ĹĹ◊≤„∂‘°į≥¨«įŌŻ∑—°ĪĶńŐ¨∂»”–≤Ó“ž£Ľ
Ń–Ń™ĪŪ£¨≤ĘĽōīū «∑Ů”–99%Ķńį—ő’»Ōő™ĶĪ‘¬ ’»Ž“‘8000‘™ő™∑÷ĹÁĶ„ Ī£¨ł√ –ĶńĻ§–ĹĹ◊≤„∂‘°į≥¨«įŌŻ∑—°ĪĶńŐ¨∂»”–≤Ó“ž£Ľ
‘¬ ’»Ž≤ĽĶÕ”ŕ8000‘™ | ‘¬ ’»ŽĶÕ”ŕ8000‘™ | ◊‹ľ∆ | |
»ŌÕ¨ | |||
≤Ľ»ŌÕ¨ | |||
◊‹ľ∆ |
£®2£©»Űī”‘¬ ’»Ž‘ŕ![]() ĶńĪĽĶų≤ť∂‘Ōů÷–ňśĽķ—°»°2»ňĹÝ––Ķų≤ť£¨«ů÷Ń…Ŕ”–1łŲ»ň≤Ľ»ŌÕ¨°į≥¨«įŌŻ∑—°ĪĶńłŇ¬ .
ĶńĪĽĶų≤ť∂‘Ōů÷–ňśĽķ—°»°2»ňĹÝ––Ķų≤ť£¨«ů÷Ń…Ŕ”–1łŲ»ň≤Ľ»ŌÕ¨°į≥¨«įŌŻ∑—°ĪĶńłŇ¬ .
≤őŅľĻę Ĺ£ļ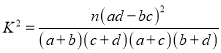 £®∆š÷–
£®∆š÷–![]() £©.
£©.
łĹĪŪ£ļ
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |