题目内容
11.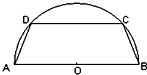 如图,有一块半径为2a(a>0)的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.记AD长为x,梯形周长为y.
如图,有一块半径为2a(a>0)的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.记AD长为x,梯形周长为y.(Ⅰ)求y关于x的函数解析式,并求出定义域;
(Ⅱ)由于钢板有特殊需要,要求CD长不小于$\frac{7}{2}a$,在此条件下,求梯形周长y的最大值.
分析 (Ⅰ)作DE⊥AB,由直角三角形的射影定理,可得AE的长,进而得到CD,令CD>0,可得x的范围,再由y=AB+BC+CD+DA,可得函数的解析式;
(Ⅱ)运用二次函数的配方,求得对称轴,由CD长不小于$\frac{7}{2}a$,可得0<x≤a,由单调性可得y的最大值.
解答 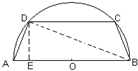 解:(Ⅰ)如图,作DE⊥AB,
解:(Ⅰ)如图,作DE⊥AB,
由已知得:$∠ADB=\frac{π}{2}$,
又AD=x,AB=4a,∴$AE=\frac{x^2}{4a}$,
∴$CD=AB-2AE=4a-\frac{x^2}{2a}$,
∴$y=AB+BC+CD+DA=4a+2x+4a-\frac{x^2}{2a}=-\frac{x^2}{2a}+2x+8a$,
又AD=x>0,$AE=\frac{x^2}{4a}>0$,$CD=4a-\frac{x^2}{2a}>0$,
∴0<x<2$\sqrt{2}$a,
所求函数为:$y=-\frac{x^2}{2a}+2x+8a$$(0<x<2\sqrt{2}a)$;
(Ⅱ)由(Ⅰ)知:$y=-\frac{x^2}{2a}+2x+8a$$(0<x<2\sqrt{2}a)$,
又$CD=4a-\frac{x^2}{2a}≥\frac{7}{2}a$,
∴0<x≤a,
又$y=-\frac{x^2}{2a}+2x+8a=-\frac{1}{2a}{(x-2a)^2}+10a$,
区间(0,a]为增区间,
∴x=a时,${y_{max}}=\frac{19}{2}a$.
点评 本题考查二次函数的应用题,主要考查函数的解析式和最值的求法,属于中档题.

练习册系列答案
相关题目
20.一个几何体的三视图如图所示,则该几何体的体积为( )
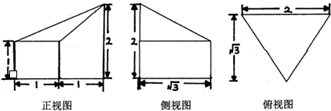

| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{4\sqrt{3}}{3}$ | D. | 2$\sqrt{3}$ |
1.对于命题:p:?x∈(0,$\frac{π}{2}$),sinx+cosx>1;q:?x∈R,sin2x+cos2x>1,则下列判断正确的是( )
| A. | p假q真 | B. | p真q假 | C. | p假q假 | D. | p真q真 |
