题目内容
16.如图在Rt△ABC中∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BD=6.4.
分析 先根据相似三角形的判定定理得出△ACD∽△ABC,再根据相似三角形的对应边成比例得到比例式后代入AC和AD的值即可求得结果.
解答 解:∵△ABC是直角三角形,CD⊥AB,
∴∠A+∠B=90°,∠A+∠ACD=90°,
∴∠B=∠ACD,
∴△ACD∽△ABC,
∴$\frac{AD}{AC}=\frac{AC}{AB}$,
∵AC=6,AD=3.6,
∴AB=10,
∴BD=10-3.6=6.4.
故答案为:6.4.
点评 本题考查的是相似三角形的判定与性质及勾股定理,根据题意判断出△ACD∽△ABC是解答此题的关键.

练习册系列答案
相关题目
6.设函数f(x)=lg(x2+ax-a-1),给出下述命题:
①函数f(x)的值域为R;
②函数f(x)有最小值;
③当a=0时,函数f(x)为偶函数;
④若f(x)在区间[2,+∞)上单调递增,则实数a的取值范围a≥-4.
正确的命题是( )
①函数f(x)的值域为R;
②函数f(x)有最小值;
③当a=0时,函数f(x)为偶函数;
④若f(x)在区间[2,+∞)上单调递增,则实数a的取值范围a≥-4.
正确的命题是( )
| A. | ①③④ | B. | ②③ | C. | ②④ | D. | ①③ |
8.已知f1(x)=sinx+cosx,f n+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,f n+1(x)=fn′(x),n∈N*,则f1(x)+f2(x)+…+f 2011(x)=( )
| A. | -sinx+cosx | B. | sinx-cosx | C. | -sinx-cosx | D. | sinx+cosx |
5.在所有两位数(10~99)中,任取一个数,能被2或3整除的概率是( )
| A. | $\frac{5}{6}$ | B. | $\frac{4}{5}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{2}$ |
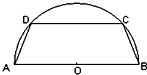 如图,有一块半径为2a(a>0)的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.记AD长为x,梯形周长为y.
如图,有一块半径为2a(a>0)的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.记AD长为x,梯形周长为y.