题目内容
3.求下列各题中的函数f(x)的解析式.(1)已知f($\sqrt{x}+2$)=x+4$\sqrt{x}$,求f(x)
(2)已知函数t=f(x)满足2f(x)+f($\frac{1}{x}$)=2x,x∈R且x≠0,求f(x)
分析 (1)利用换元法设t=$\sqrt{x}$+2(t≥2),则$\sqrt{x}$=t-2,代入求出即可;(2)将x换成$\frac{1}{x}$,则$\frac{1}{x}$换成x,解出f(x)即可.
解答 解:(1)设t=$\sqrt{x}$+2(t≥2),则$\sqrt{x}$=t-2,即x=(t-2)2,
∴f(t)=(t-2)2+4(t-2)=t2-4,
∴f(x)=x2-4(x≥2).
(2)由2f(x)+f($\frac{1}{x}$)=2x,①
将x换成$\frac{1}{x}$,则$\frac{1}{x}$换成x,得2f($\frac{1}{x}$)+f(x)=$\frac{2}{x}$,②
①×2-②,得3f(x)=4x-$\frac{2}{x}$,
∴f(x)=$\frac{4}{3}$x-$\frac{2}{3x}$.
点评 本题考查了求函数的解析式问题,换元法是常用方法之一,本题是一道基础题.

练习册系列答案
相关题目
18.已知△ABC中,$a=\sqrt{2}$,$b=\sqrt{3}$,B=60°,那么∠A=( )
| A. | 45° | B. | 90° | C. | 135°或45° | D. | 150°或30° |
8.已知f1(x)=sinx+cosx,f n+1(x)是fn(x)的导函数,即f2(x)=f1′(x),f3(x)=f2′(x),…,f n+1(x)=fn′(x),n∈N*,则f1(x)+f2(x)+…+f 2011(x)=( )
| A. | -sinx+cosx | B. | sinx-cosx | C. | -sinx-cosx | D. | sinx+cosx |
12.在△ABC中,E,F分别为AB,AC的中点,则有EF∥BC.这个命题的大前提为( )
| A. | 三角形的中位线平行于第三边 | B. | 三角形的中位线等于第三边的一半 | ||
| C. | EF为中位线 | D. | EF∥CB |
13. 如图,某大风车的半径为2m,每6s旋转一周,它的最低点O离地面0.5 m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m),则函数h=f(t)的关系式( )
如图,某大风车的半径为2m,每6s旋转一周,它的最低点O离地面0.5 m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m),则函数h=f(t)的关系式( )
 如图,某大风车的半径为2m,每6s旋转一周,它的最低点O离地面0.5 m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m),则函数h=f(t)的关系式( )
如图,某大风车的半径为2m,每6s旋转一周,它的最低点O离地面0.5 m.风车圆周上一点A从最低点O开始,运动t(s)后与地面的距离为h(m),则函数h=f(t)的关系式( )| A. | y=-2cos$\frac{πt}{6}$+2.5 | B. | y=-2sin$\frac{πt}{6}$+2.5 | C. | y=-2cos$\frac{πt}{3}$+2.5 | D. | y=-2sin$\frac{πt}{3}$+2.5 |
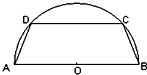 如图,有一块半径为2a(a>0)的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.记AD长为x,梯形周长为y.
如图,有一块半径为2a(a>0)的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上.记AD长为x,梯形周长为y.