题目内容
1.化简:$\frac{\sqrt{(4+\sqrt{15})^{3}}+\sqrt{(4-\sqrt{15})^{3}}}{\sqrt{(6+\sqrt{35})^{3}}-\sqrt{(6-\sqrt{35})^{3}}}$=$\frac{7}{13}$.分析 直接利用立方和与立方差公式化简求解即可.
解答 解:$\frac{\sqrt{{(4+\sqrt{15})}^{3}}+\sqrt{{(4-\sqrt{15})}^{3}}}{\sqrt{{(6+\sqrt{35})}^{3}}-\sqrt{{(6-\sqrt{35})}^{3}}}$=$\frac{(\sqrt{4+\sqrt{15}}+\sqrt{4-\sqrt{15}})(4+\sqrt{15}-\sqrt{(4+\sqrt{15})(4-\sqrt{15})}+4-\sqrt{15})}{(\sqrt{6+\sqrt{35}}-\sqrt{6-\sqrt{35}})(6+\sqrt{35}+\sqrt{(6+\sqrt{35})(6-\sqrt{35})}+6-\sqrt{35})}$
=$\frac{7(\sqrt{4+\sqrt{15}}+\sqrt{4-\sqrt{15}})}{13(\sqrt{6+\sqrt{35}}-\sqrt{6-\sqrt{35}})}$
=$\frac{7}{13}\sqrt{\frac{(\sqrt{4+\sqrt{15}}+\sqrt{4-\sqrt{15}})^{2}}{(\sqrt{6+\sqrt{35}}-\sqrt{6-\sqrt{35}})^{2}}}$
=$\frac{7}{13}\sqrt{\frac{8+2}{12-2}}$=$\frac{7}{13}$.
故答案为:$\frac{7}{13}$.
点评 本题考查根式以及有理指数幂的运算法则的应用,考查计算能力.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
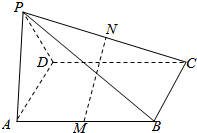 如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.
如图,四棱锥P-ABCD的底面ABCD是平行四边形,M、N分别是AB、PC的中点,且MN⊥PC,MN⊥AB.证明:平面PAD⊥平面PDC.