题目内容
10.已知函数f(x)=ax+$\frac{a-1}{x}$+(1-2a)(a>0)(1)当a≥$\frac{1}{2}$时,比较f(x)与㏑x在[1,+∞)上的大小关系;
(2)证明:1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$>㏑(n+1)+$\frac{n}{{2({n+1})}}$(n≥1);
(3)已知S=1+$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2014}$,求S的整数部分.(ln2014≈7.6079,ln2015≈7.6084)
分析 (1)令g(x)=f(x)-lnx,利用导数研究其单调性即可得出.
( II)由( I)可知:当$a≥\frac{1}{2}$时,有f(x)≥lnx(x≥1),令$a=\frac{1}{2}$,有$f(x)=\frac{1}{2}(x-\frac{1}{x})≥lnx(x≥1)$,且当$x>1时,\frac{1}{2}(x-\frac{1}{x})>lnx$,令$x=\frac{k+1}{k},有ln\frac{k+1}{k}<\frac{1}{2}[{\frac{k-1}{k}-\frac{k}{k+1}}]=\frac{1}{2}[{(1+\frac{1}{k})-(1-\frac{1}{k+1})}]$,即$ln(k+1)-lnk<\frac{1}{2}(\frac{1}{k}+\frac{1}{k+1}),k=1,2,3,…n$,利用“累加求和”即可得出.
(3)重要不等式$\frac{x}{1+x}≤ln(1+x)$,令$x=\frac{1}{n-1}$,得$\frac{1}{n}<lnn-ln(n-1)$,通过累加可得1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$<1+lnn,于是1+lnn>1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$>㏑(n+1)+$\frac{n}{{2({n+1})}}$,利用已知即可得出.
解答 解:(1)令$g(x)=f(x)-lnx=ax+\frac{a-1}{x}+1-2a-lnx,x∈[{1,+∞})$,
则$g(1)=0,g'(x)=a-\frac{a-1}{x^2}-\frac{1}{x}=\frac{{a{x^2}-x-(a-1)}}{x^2}=\frac{{a(x-1)(x-\frac{1-a}{a})}}{x^2}$,
当$a≥\frac{1}{2}时,\frac{1-a}{a}≤1$.
∵x>1,则g'(x)>0,g(x)是增函数,
∴g(x)>g(1)=0,
即f(x)>lnx.
( II)由( I)可知:当$a≥\frac{1}{2}$时,有f(x)≥lnx(x≥1),
令$a=\frac{1}{2}$,有$f(x)=\frac{1}{2}(x-\frac{1}{x})≥lnx(x≥1)$,且当$x>1时,\frac{1}{2}(x-\frac{1}{x})>lnx$,
令$x=\frac{k+1}{k},有ln\frac{k+1}{k}<\frac{1}{2}[{\frac{k-1}{k}-\frac{k}{k+1}}]=\frac{1}{2}[{(1+\frac{1}{k})-(1-\frac{1}{k+1})}]$,
即$ln(k+1)-lnk<\frac{1}{2}(\frac{1}{k}+\frac{1}{k+1}),k=1,2,3,…n$,
将上述n个不等式依次相加得$ln(n+1)<\frac{1}{2}+(\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n})+\frac{1}{2(n+1)}$.
整理得$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}>ln(n+1)+\frac{n}{2(n+1)}$.
(3)重要不等式$\frac{x}{1+x}≤ln(1+x)$,令$x=\frac{1}{n-1}$,得$\frac{1}{n}<lnn-ln(n-1)$,
通过累加可得1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$<1+lnn,
所以1+lnn>1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$>㏑(n+1)+$\frac{n}{{2({n+1})}}$,
令n=2014,得1+ln2014>S>ln2015+$\frac{1007}{2015}$,
1+ln2014≈8.6079,ln2015+$\frac{1007}{2015}$≈7.6084+0.4948=8.1032,
∴S的整数部分是8.
点评 本题考查了利用导数研究函数的单调性极值与最值及其证明不等式、“放缩法”、对数的运算性质,考查了推理能力与计算能力,属于难题.

| A. | 命题“p或q”为假 | B. | 命题“p且q“为真 | ||
| C. | 命题,“¬p或q”为假 | D. | 命题“p且¬q“为假 |
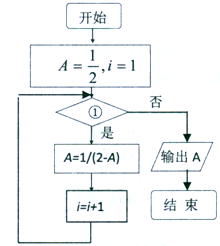 如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )
如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )| A. | i≤3 | B. | i≤4 | C. | i≤5 | D. | i≤6 |
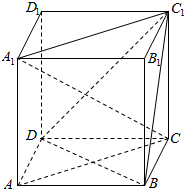 如图,在边长为1的正方体ABCD-A1B1C1D1中,求证:
如图,在边长为1的正方体ABCD-A1B1C1D1中,求证: