题目内容
16.设函数f(x)=alnx-2ax+3(a≠0)(1)设a=-1,求f(x)的极值;
(2)在(1)的条件下,若g(x)=$\frac{1}{3}$x3+x2[f′(x)+m]在(1,3)上不是单调函数,求m的范围;
(3)求f(x)=(x-3)ex的单调递增区间.
分析 (1)先求函数的导函数f′(x),再解不等式f′(x)>0,得函数的单调增区间,解不等式f′(x)<0得函数的单调减区间,最后由极值定义求得函数极值.
(2)构造新函数g(x),把在区间(1,3)上不是单调函数,即函数g(x)的导函数在区间(1,3)不能恒为正或恒为负,从而转化为求导函数的函数值问题,利用导数列出不等式,最后解不等式求得实数m的取值范围.
(3)求函数的导数,解不等式f′(x)>0即可.
解答 解:(1)当a=-1,f(x)=-lnx+2x+3(x>0),${f^'}(x)=\frac{-1}{x}+2$,…(2分)
∴f(x)的单调递减区间为(0,$\frac{1}{2}$),单调递增区间为($\frac{1}{2}$,+∞) …(4分),
∴f(x)的极小值是$f(\frac{1}{2})=-ln\frac{1}{2}+2×\frac{1}{2}+3=ln2+4$.…(6分)
(2)$g(x)=\frac{1}{3}{x}^{3}+{x}^{2}(-\frac{1}{x}+2+m)$,g′(x)=x2+(4+2m)x-1,…(8分)
∴g(x)在区间(1,3)上不是单调函数,
且g′(0)=-1,
∴$\left\{\begin{array}{l}{g′(1)<0}\\{g′(3)>0}\end{array}\right.$ …(10分)
∴$\left\{\begin{array}{l}{4+2m<0}\\{20+6m>0}\end{array}\right.$,
即:-$\frac{10}{3}<m<-2$.
故m的取值范围$(-\frac{10}{3},-2)$…(12分)
(3)∵f(x)=(x-3)ex,
∴f′(x)=(x-3)′ex+(x-3)(ex)′=(x-2)ex,
令f′(x)>0,解得x>2.
即函数单调递增区间为(2,+∞).
点评 本题考查了函数的定义域、单调性、极值,以及导数在其中的应用,由不等式恒成立问题与最值问题求解参数的取值范围的方法.

| A. | 37 | B. | 36 | C. | 26 | D. | 7 |
| A. | 命题“p或q”为假 | B. | 命题“p且q“为真 | ||
| C. | 命题,“¬p或q”为假 | D. | 命题“p且¬q“为假 |
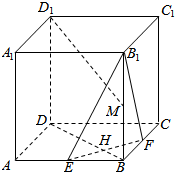 如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证:
如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证: