题目内容
13．已知a、b、c分别为一个三角形的三边长，求证：$\frac{c}{a+b}$+$\frac{a}{b+c}$+$\frac{b}{c+a}$＜2．分析 利用“$\frac{a}{b+c}$＜$\frac{a+a}{b+c+a}$”放缩可知$\frac{a}{b+c}$＜$\frac{2a}{a+b+c}$、$\frac{b}{c+a}$＜$\frac{2b}{a+b+c}$、$\frac{c}{a+b}$＜$\frac{2c}{a+b+c}$，相加计算即得结论．
解答 证明：依题意易知$\frac{c}{a+b}$、$\frac{a}{b+c}$、$\frac{b}{c+a}$均为正分数，
∴$\frac{a}{b+c}$＜$\frac{a+a}{b+c+a}$=$\frac{2a}{a+b+c}$，
同理可知$\frac{b}{c+a}$＜$\frac{2b}{a+b+c}$，$\frac{c}{a+b}$＜$\frac{2c}{a+b+c}$，
∴$\frac{c}{a+b}$+$\frac{a}{b+c}$+$\frac{b}{c+a}$＜$\frac{2c}{a+b+c}$+$\frac{2a}{a+b+c}$+$\frac{2b}{a+b+c}$
=$\frac{2（a+b+c）}{a+b+c}$
=2．
点评 本题考查不等式的证明，利用不等式的性质是解决本题的关键，注意解题方法的积累，属于中档题．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
5．若命题p：?x∈R，x＞lnx-2，命题q：?x∈R，2x＞1，那么（ ）
| A． | 命题“p或q”为假 | B． | 命题“p且q“为真 | ||
| C． | 命题，“￢p或q”为假 | D． | 命题“p且￢q“为假 |
2．
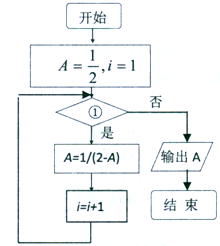如图所示的程序框图，若执行后的结果是$\frac{5}{6}$，则在①处应填写的是（ ）
如图所示的程序框图，若执行后的结果是$\frac{5}{6}$，则在①处应填写的是（ ）| A． | i≤3 | B． | i≤4 | C． | i≤5 | D． | i≤6 |
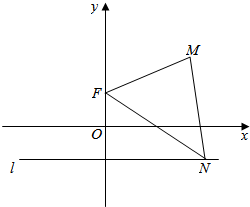如图，已知点F（0，p），直线l：y=-p（其中p为常数，且p＞0），M为平面内的动点，过M作l的垂线，垂足为N，且$\overrightarrow{NM}•\overrightarrow{NF}$=$\overrightarrow{FM}•\overrightarrow{FN}$．