题目内容
12.讨论复合函数y=$\sqrt{5-4x-{x}^{2}}$的单调性.分析 令t=5-4x-x2≥0,可得函数y的定义域、y=$\sqrt{t}$,本题即求函数t在定义域内的单调性.再利用二次函数的性质可得t=5-4x-x2在定义域内的单调区间.
解答 解:令t=5-4x-x2≥0,可得函数y的定义域为{x|-5≤x≤1},且y=$\sqrt{t}$,
故本题即求函数y=$\sqrt{5-4x-{x}^{2}}$的在定义域内的单调性.
再利用二次函数的性质可得t=5-4x-x2的图象的对称轴为x=-2,
可得函数t在定义域内的增区间为[-5,-2),减区间为[-2,1].
故函数y的增区间为[-5,-2),减区间为[-2,1].
点评 本题主要考查复合函数的单调性、二次函数的性质,体现了转化的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.设集合A={x|2x-x2>0},B={x|x>1},R为实数集,则(∁RB)∩A等于( )
| A. | (0,1) | B. | [1,2) | C. | (0,1] | D. | (-∞,0) |
2.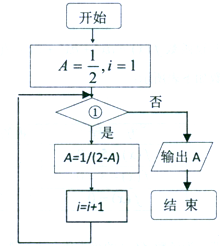 如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )
如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )
 如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )
如图所示的程序框图,若执行后的结果是$\frac{5}{6}$,则在①处应填写的是( )| A. | i≤3 | B. | i≤4 | C. | i≤5 | D. | i≤6 |
 如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证:
如图,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别为AB和BC的中点,M为棱B1B的中点.求证: