题目内容
【题目】如图,在三棱柱ABCA1B1C1中,BC=BB1,∠BAC=∠BCA=![]() ∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.
∠ABC,点E是A1B与AB1的交点,点D在线段AC上,B1C∥平面A1BD.
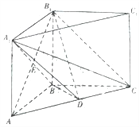
(1)求证:BD⊥A1C;
(2)求证:AB1⊥平面A1BC。
【答案】(1)见解析(2)见解析
【解析】试题分析:(1)先根据线面平行性质定理得B1C//ED,再根据等腰三角形性质得BD⊥AC,根据直棱柱性质得A1A⊥BD,最后根据线面垂直判定定理得结论,(2)根据菱形性质得AB1⊥A1B,再根据直棱柱性质得BC⊥BB1, 由AB⊥BC,根据线面垂直判定定理得BC⊥平面ABB1A.即得BC⊥AB1,最后根据线面垂直判定定理得结论.
试题解析:
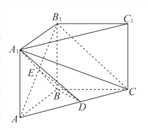
(I)证明:连结ED,∵平面AB1C![]() 平面A1BD=ED,B1C//平面A1BD,
平面A1BD=ED,B1C//平面A1BD,
∴B1C//ED,.
∵E为AB1中点,∴D为AC中点;..
∵∠BAC=∠BCA=![]() ∠ABC,∴AB=BC,∴BD⊥AC,.
∠ABC,∴AB=BC,∴BD⊥AC,.
由A1A⊥平面ABC,BD![]() 平面ABC,得A1A⊥BD.
平面ABC,得A1A⊥BD.
由及A1A、AC是平面A1ACC1内的两条相交直线,
得BD⊥平面A1ACC1,
因为A1C![]() 平面AlACC1,故BD⊥A1C
平面AlACC1,故BD⊥A1C
(Ⅱ)由(Ⅰ)知AB=BC,AB⊥BC,.
∵BB1=BC,∴四边形ABB1A1是菱形,∴AB1⊥A1B,.
∵BB1⊥平面ABC,BC![]() 平面ABC.∴BC⊥BB1.
平面ABC.∴BC⊥BB1.
∵AB![]() BB1=B,AB,BB1
BB1=B,AB,BB1![]() 平面ABB1A1.∴BC⊥平面ABB1A..
平面ABB1A1.∴BC⊥平面ABB1A..
∵AB1![]() 平面ABB1A1,∴BC⊥AB1,....
平面ABB1A1,∴BC⊥AB1,....
∵BC![]() A1B=B,BC,A1B
A1B=B,BC,A1B![]() 平面A1BC,∴AB1⊥平面A1BC.
平面A1BC,∴AB1⊥平面A1BC.
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行,需转化为证明线线平行.
(2)证明线面垂直,需转化为证明线线垂直.
(3)证明线线垂直,需转化为证明线面垂直.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案