题目内容
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() .已知点
.已知点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在
在![]() 上,
上, ![]() 是边长为4的等边三角形.
是边长为4的等边三角形.
(1)求![]() 的值;
的值;
(2)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,当过点
,当过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点时,
两点时, ![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由题知, ![]() ,则
,则![]() .设准线
.设准线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]() .又
.又![]() 是边长为4的等边三角形,
是边长为4的等边三角形, ![]() ,所以
,所以![]() ,
, ![]() ,从而可得结果;(2)设点
,从而可得结果;(2)设点![]() ,由题意知直线
,由题意知直线![]() 的斜率不为零,设直线
的斜率不为零,设直线![]() 的方程为
的方程为![]() ,
,
由![]() 得,
得, ![]() ,由韦达定理及两点间距离公式可得
,由韦达定理及两点间距离公式可得![]() ,同理可得
,同理可得![]() ,化简即可得
,化简即可得 ,
, ![]() 时
时![]() 为定值,此时点
为定值,此时点![]() 为定点.
为定点.
试题解析:(1)由题知, ![]() ,则
,则![]() .设准线
.设准线![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]() .又
.又![]() 是边长为4的等边三角形,
是边长为4的等边三角形, ![]() ,所以
,所以![]() ,
, ![]() ,即
,即![]() .
.
(2)设点![]() ,由题意知直线
,由题意知直线![]() 的斜率不为零,
的斜率不为零,
设直线![]() 的方程为
的方程为![]() ,点
,点![]() ,
, ![]() ,
,
由![]() 得,
得, ![]() ,则
,则![]() ,
, ![]() ,
, ![]() .
.
又![]() ,同理可得
,同理可得![]() ,则有
,则有![]()



 .
.
若![]() 为定值,则
为定值,则![]() ,此时点
,此时点![]() 为定点.
为定点.
又当![]() ,
, ![]() 时,
时, ![]() ,
,
所以,存在点![]() ,当过点
,当过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点时,
两点时, ![]() 为定值
为定值![]() .
.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象时,列表并填入了部分数据,如下表:
在某一个周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(1)请将上表数据补充完整,填写在相应位置,并求出函数![]() 的解析式;
的解析式;
(2)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
【题目】假设关于某种设备的使用年限![]() (年)与所支出的维修费用
(年)与所支出的维修费用![]() (万元)有如下统计:
(万元)有如下统计:
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知![]() ,
, ![]() .
. 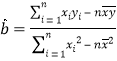 ,
, ![]()
(1)求![]() ,
, ![]() ;
;
(2)![]() 与
与![]() 具有线性相关关系,求出线性回归方程;
具有线性相关关系,求出线性回归方程;
(3)估计使用年限为10年时,维修费用约是多少?