题目内容
【题目】已知抛物线E：
的焦点为F，
是抛物线E上一点，且
．
1
求抛物线E的标准方程；
2设点B是抛物线E上异于点A的任意一点，直线AB与直线
交于点P，过点P作x轴的垂线交抛物线E于点M，设直线BM的方程为
，k，b均为实数，请用k的代数式表示b，并说明直线BM过定点．
【答案】（1）
；（2）见解析
【解析】
1
利用抛物线的定义与性质求p的值，即可写出抛物线方程；2设点
，
，由直线BM的方程和抛物线方程联立，消去y，利用根与系数的关系和A，P，B三点共线，化简整理可得BM的方程，从而求出直线BM所过的定点．
解：1根据题意知，
，①
因为
，所以
，②
联立①②解得
，
；
所以抛物线E的标准方程为；
2设，；
又直线BM的方程为
，代入，得
；
由根与系数的关系，得
，
；③
由
轴及点P在直线
上，得
，
则由A，P，B三点共线，得
，
整理，得
；
将③代入上式并整理，得
，
由点B的任意性，得
，即
，
所以
；
即直线BM恒过定点
．
练习册系列答案
相关题目
【题目】假设关于某种设备的使用年限
(年)与所支出的维修费用
(万元)有如下统计：
| 2 | 3 | 4 | 5 | 6 |
| 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
已知
， 
. 
， 
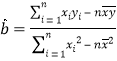(1)求
， 
；
(2)与具有线性相关关系，求出线性回归方程；
(3)估计使用年限为10年时，维修费用约是多少？
