题目内容
8.已知椭圆C的焦点是F1(-2$\sqrt{2}$,0}),F2(2$\sqrt{2}$,0),其上的动点P满足|PF1|+|PF2|=4$\sqrt{3}$.点O为坐标原点,椭圆C的下顶点为R.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设过点(0,1)且斜率为k的直线l2交椭圆C于M,N两点,试证明:无论k取何值,$\overrightarrow{RM}$•$\overrightarrow{RN}$恒为定值.
分析 (Ⅰ)由题意设出椭圆方程,由已知求得a,结合隐含条件求得b,则椭圆方程可求;
(Ⅱ)写出直线l2的方程,联立直线方程和椭圆方程,利用根与系数的关系得到M,N两点横坐标的和与积,由向量数量积的坐标表示求得$\overrightarrow{RM}$•$\overrightarrow{RN}$恒为定值.
解答 (Ⅰ)解:设椭圆的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0).
∵$|{P{F_1}}|+|{P{F_2}}|=4\sqrt{3}$,∴$2a=4\sqrt{3}$,a=$2\sqrt{3}$.
又$c=2\sqrt{2}$,∴a2=12,b2=a2-c2=4,
∴椭圆C的标准方程为$\frac{x^2}{12}+\frac{y^2}{4}=1$;
(Ⅱ)证明:设l2:y=kx+1,联立方程组$\left\{\begin{array}{l}y=kx+1\\{x^2}+3{y^2}-12=0\end{array}\right.$,
消去y得(1+3k2)x2+6kx-9=0,
又∵点(0,1)在椭圆C内,∴△>0恒成立.
设M (x1,kx1+1),N(x2,x2+1),
则${x_1}+{x_2}=\frac{-6k}{{1+3{k^2}}}$,${x_1}{x_2}=\frac{-9}{{1+3{k^2}}}$,
易知R(0,-2),$\overrightarrow{RM}$=(x1,kx1+3),$\overrightarrow{RN}$=(x2,kx2+3),
∴$\overrightarrow{RM}$•$\overrightarrow{RN}$=x1x2+(kx1+3)(kx2+3)=(1+k2)x1x2+3k(x1+x2)+9
=(1+k2)•$\frac{-9}{{1+3{k^2}}}$+3k•$\frac{-6k}{{1+3{k^2}}}$+9=0,与k无关.
点评 本题考查椭圆的简单性质,考查了直线和圆锥曲线间的关系,考查平面向量数量积的坐标表示,是中档题.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案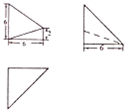 已知某空间几何体的三视图如图所示,则该几何体的体积是( )
已知某空间几何体的三视图如图所示,则该几何体的体积是( )| A. | 16 | B. | 32 | C. | 36 | D. | 48 |
| A. | $\sqrt{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 1 | D. | $\frac{{\sqrt{2}}}{2}$ |
| A. | [1,2) | B. | [1,2] | C. | (2,3] | D. | [2.3] |
| A. | (1,4] | B. | (2,4) | C. | [2,4) | D. | (4,+∞) |
| A. | -i | B. | -1 | C. | i | D. | 1 |