题目内容
抛物线的弦与过弦的端点的两条切线所围成的三角形常被称为阿基米德三角形,阿基米德三角形有一些有趣的性质,如:若抛物线的弦过焦点,则过弦的端点的两条切线的交点在其准线上.设抛物线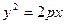
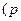 >
> ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
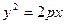
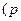 >
>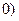 ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为A.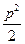 | B.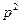 | C.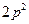 | D.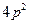 |
B
略

练习册系列答案
相关题目
题目内容
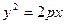
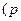 >
>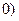 ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为A.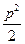 | B.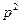 | C.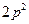 | D.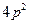 |
