题目内容
(本小题满分14分)
已知焦点在x轴上,离心率为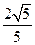 的椭圆的一个顶点是抛物线
的椭圆的一个顶点是抛物线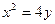 的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且
的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且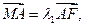
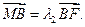
(1)求椭圆的方程;
(2)证明: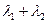 为定值。
为定值。
已知焦点在x轴上,离心率为
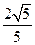 的椭圆的一个顶点是抛物线
的椭圆的一个顶点是抛物线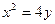 的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且
的焦点,过椭圆右焦点F的直线l交椭圆于A、B两点,交y轴于点M,且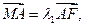
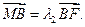
(1)求椭圆的方程;
(2)证明:
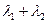 为定值。
为定值。(1)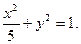
(2)证明见解析。
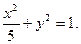
(2)证明见解析。
(1)依题意,设椭圆方程为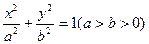 (1分)
(1分)
因为抛物线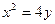 的焦点为(0,1),所以
的焦点为(0,1),所以 (2分)
(2分)
由 (4分)
(4分)
故椭圆方程 为
为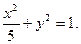 (5分)
(5分)
(2)依题意设A、B、M的坐标分别为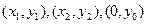 ,
,
由(1)得椭圆的右焦点F(2,0), (6分)
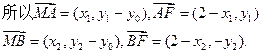
由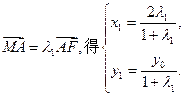 (8分)
(8分)
由 (10分)
(10分)
因为A、B在椭圆上,所以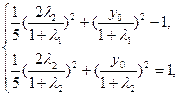
即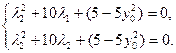 (12分)
(12分)
所以 的两根,
的两根,
故 是定值。 (14分)
是定值。 (14分)
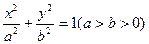 (1分)
(1分)因为抛物线
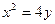 的焦点为(0,1),所以
的焦点为(0,1),所以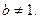 (2分)
(2分)由
 (4分)
(4分)故椭圆方程
 为
为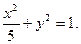 (5分)
(5分)(2)依题意设A、B、M的坐标分别为
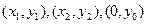 ,
,由(1)得椭圆的右焦点F(2,0), (6分)
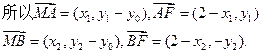
由
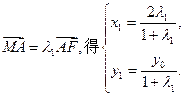 (8分)
(8分)由
 (10分)
(10分)因为A、B在椭圆上,所以
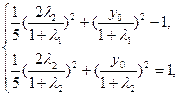
即
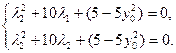 (12分)
(12分)所以
 的两根,
的两根,故
 是定值。 (14分)
是定值。 (14分)
练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 的外接圆
的外接圆 与
与 轴交于点
轴交于点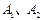 ,椭圆
,椭圆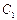 以线段
以线段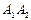
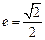 .
.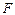 ,点
,点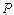 为圆
为圆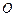 作直线
作直线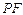 的垂线交直线
的垂线交直线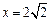 于点
于点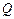 ,判断直线
,判断直线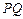 与圆
与圆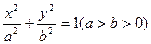 引两条切线,切点分别为B,C,且
引两条切线,切点分别为B,C,且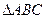 为正三角形.
为正三角形. 最大时椭圆的方程;
最大时椭圆的方程; ,过
,过 与
与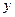 轴交于点
轴交于点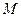 ,与椭圆的一个交点为
,与椭圆的一个交点为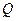 ,且
,且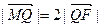 求直线
求直线 的准线上,则p的值为 。
的准线上,则p的值为 。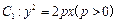 的焦点
的焦点 恰好是曲线
恰好是曲线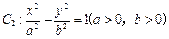 的右焦点,且
的右焦点,且 与
与 交点的连线过点
交点的连线过点
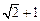

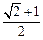
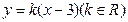 与双曲线
与双曲线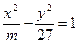 。某学生做了如下变形:由方程组
。某学生做了如下变形:由方程组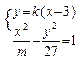 ,消去
,消去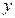 后得到形如
后得到形如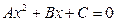 的方程。当
的方程。当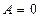 时,该方程有一解,当
时,该方程有一解,当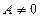 时,
时,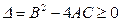 恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )
恒成立。假设该学生的演算过程是正确的,则实数m的取值范围是 ( )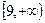
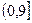
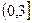
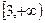
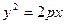
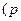 >
>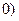 ,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为
,弦AB过焦点,△ABQ为其阿基米德三角形,则△ABQ的面积的最小值为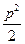
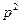
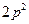
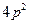
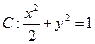 的左焦点为
的左焦点为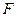 ,左准线为
,左准线为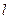 ,点
,点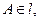 线段
线段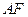 交椭圆
交椭圆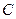 于点
于点 ,若
,若 ,则
,则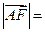 _____________.
_____________.