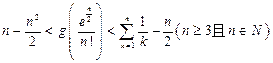题目内容
设函数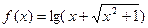 .
.
(1)确定函数f (x)的定义域;
(2)证明函数f (x)在其定义域上是单调增函数。
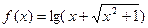 .
.(1)确定函数f (x)的定义域;
(2)证明函数f (x)在其定义域上是单调增函数。
(1)R(2)(3)
(1)由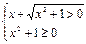 得x∈R,定义域为R. …………2分
得x∈R,定义域为R. …………2分
(2)设x1,x2∈R,且x1<x2,
则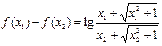 . 令
. 令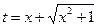 ,
,
则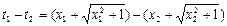 . =
. =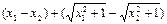
=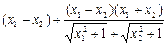 =
=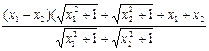
∵x1-x2<0,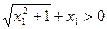 ,
,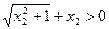 ,
,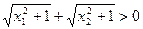 ,
,
∴t1-t2<0,∴0<t1<t2,∴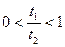 ,…………12分
,…………12分
∴f (x1)-f (x2)<lg1=0,即f (x1)<f (x2),∴ 函数f(x)在R上是单调增函数
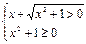 得x∈R,定义域为R. …………2分
得x∈R,定义域为R. …………2分(2)设x1,x2∈R,且x1<x2,
则
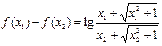 . 令
. 令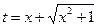 ,
,则
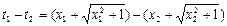 . =
. =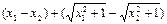
=
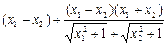 =
=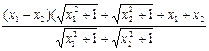
∵x1-x2<0,
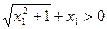 ,
,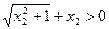 ,
,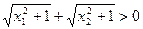 ,
,∴t1-t2<0,∴0<t1<t2,∴
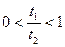 ,…………12分
,…………12分∴f (x1)-f (x2)<lg1=0,即f (x1)<f (x2),∴ 函数f(x)在R上是单调增函数

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
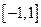 上的奇函数
上的奇函数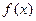 , 当
, 当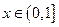 时,
时, 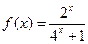 .
.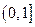 上是减函数;
上是减函数;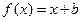 ,在
,在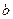 的取值范围.
的取值范围.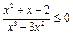 求函数
求函数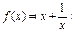 |的最小值。
|的最小值。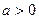 ,
,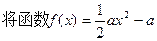 的图象向右平移
的图象向右平移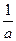 个单位再向下平移
个单位再向下平移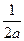 个单位后得到函数
个单位后得到函数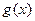 的图象。
的图象。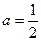 时,求
时,求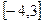 上的最大值与最小值;
上的最大值与最小值;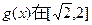 上的最小值为
上的最小值为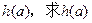 的最大值。
的最大值。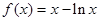 的单调递减区间为_______
的单调递减区间为_______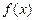 的图象;
的图象;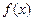 的单调递增区间.
的单调递增区间.
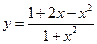 的值域.
的值域.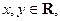 且满足
且满足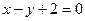 ,则
,则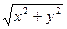 的最小值为 ;若
的最小值为 ;若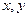 又满足
又满足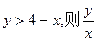 的取值范围是 .
的取值范围是 .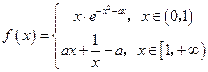 .
.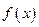 在
在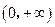 上是增函数,求实数的范围;
上是增函数,求实数的范围; 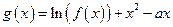 ,求证:
,求证: