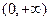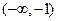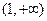题目内容
已知定义在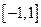 上的奇函数
上的奇函数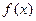 , 当
, 当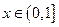 时,
时,
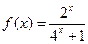 .
.
(1)求函数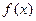 在
在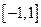 上的解析式;
上的解析式;
(2)试用函数单调性定义证明: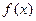 在
在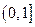 上是减函数;
上是减函数;
(3)要使方程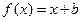 ,在
,在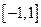 上恒有实数解,求实数
上恒有实数解,求实数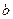 的取值范围.
的取值范围.
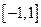 上的奇函数
上的奇函数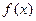 , 当
, 当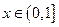 时,
时, 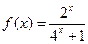 .
.(1)求函数
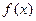 在
在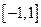 上的解析式;
上的解析式;(2)试用函数单调性定义证明:
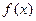 在
在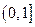 上是减函数;
上是减函数;(3)要使方程
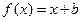 ,在
,在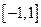 上恒有实数解,求实数
上恒有实数解,求实数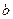 的取值范围.
的取值范围.(1)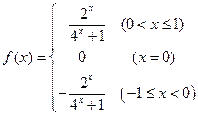 (2)见解析(3)
(2)见解析(3)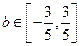
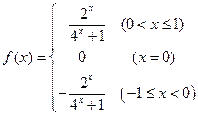 (2)见解析(3)
(2)见解析(3)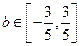
(1)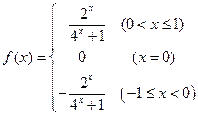
(2)证:设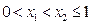 则
则
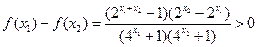
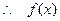 在
在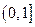 上是减函数.
上是减函数.
(3)方程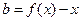 在
在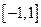 上恒有实数解,
上恒有实数解,
记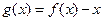 ,则
,则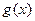 为
为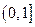 上的单调递减函数.
上的单调递减函数.
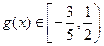
由于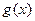 为
为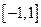 上奇函数,故当
上奇函数,故当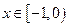 时
时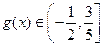
而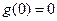
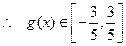 即
即 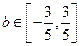 .
.
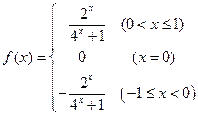
(2)证:设
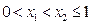 则
则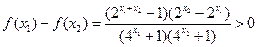
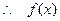 在
在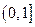 上是减函数.
上是减函数. (3)方程
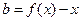 在
在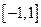 上恒有实数解,
上恒有实数解,记
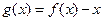 ,则
,则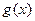 为
为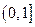 上的单调递减函数.
上的单调递减函数.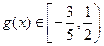
由于
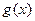 为
为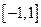 上奇函数,故当
上奇函数,故当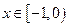 时
时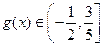
而
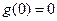
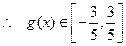 即
即 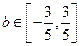 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
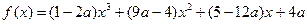 (
(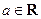 ).
).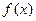 的单调递增区间;
的单调递增区间; 中,满足 “对
中,满足 “对 ,当
,当 时,都有
时,都有 ”的是
”的是 B.
B. C.
C. D.
D.
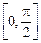 上的最大值为_________;在区间[0,2π]上最大值为___________.
上的最大值为_________;在区间[0,2π]上最大值为___________. 是
是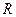 上的减函数,且
上的减函数,且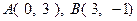 ,则当不等式
,则当不等式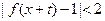 的解集为
的解集为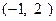 时,
时,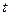 的值为
的值为 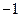
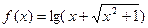 .
. ,
, ,
, ,
,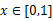
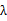 的取值范围
的取值范围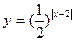 ,则它的单调区间为【 】.
,则它的单调区间为【 】.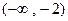 ,减区间为
,减区间为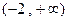
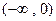 ,减区间为
,减区间为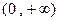
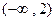 ,减区间为
,减区间为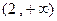
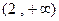 ,减区间为
,减区间为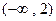
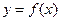 在
在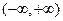 内有定义,对于给定的正数K,定义函数
内有定义,对于给定的正数K,定义函数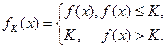
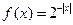 。当
。当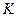 =
=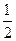 时,函数
时,函数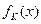 的单调递增区间为
的单调递增区间为