题目内容
【题目】已知 ![]() 是定义在
是定义在 ![]() 上的偶函数,对任意
上的偶函数,对任意 ![]() ,都有
,都有 ![]() ,且当
,且当 ![]() 时,
时, ![]() .若
.若 ![]() 在
在 ![]() 上有5个根
上有5个根 ![]() ,则
,则 ![]() 的值是( )
的值是( )
A.10
B.9
C.8
D.7
【答案】A
【解析】令 ![]() ,则方程可化为
,则方程可化为 ![]() ,依据题设问题转化为该方程有一个正实数根和一个负实数根。因为若该方程有两个正实数根,则原方程会有对应的八个实数根,所以要使原方程有五个实数根,须该方程有一个正实数根
,依据题设问题转化为该方程有一个正实数根和一个负实数根。因为若该方程有两个正实数根,则原方程会有对应的八个实数根,所以要使原方程有五个实数根,须该方程有一个正实数根 ![]() 和一个实数根
和一个实数根 ![]() 。运用题设条件可得
。运用题设条件可得 ![]() ,则函数
,则函数 ![]() 是周期
是周期 ![]() 的周期函数。依据周期性与对称性画出该函数在区间
的周期函数。依据周期性与对称性画出该函数在区间 ![]() 上的图象如上图,结合图形可以看出:当该方程有一个正实数根时,其所有根(共4根)之和为
上的图象如上图,结合图形可以看出:当该方程有一个正实数根时,其所有根(共4根)之和为 ![]() ,当有一个负实数根
,当有一个负实数根 ![]() 时,原方程只有一个根
时,原方程只有一个根 ![]() ,故原方程的所有实数根之和为
,故原方程的所有实数根之和为 ![]() , 故答案为:A。
, 故答案为:A。
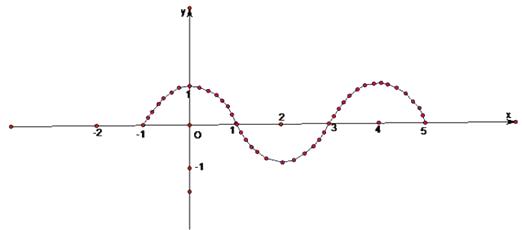
根据题设条件中的函数构成的方程有五个根,利用函数图像的对称性、奇偶性、作出函数在区间 [ 1 , 5 ] 上的图象,然后再借助对称性分析探求根的和即可得出结果。

练习册系列答案
相关题目
