题目内容
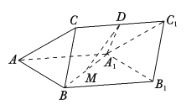
【题目】如图,三棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点, ![]() 是边长为2 的正三角形,
是边长为2 的正三角形, ![]() .
.
(1)证明: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1)取AB的中点H,连接HM,CH,证明四边形CDMH是平行四边形得出DM∥CH,从而有DM∥平面ABC;
(2)取BB1中点E,以E为原点建立坐标系,求出两半平面的法向量,计算法向量的夹角即可得出二面角的大小.
试题解析:(1)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() 分别为
分别为![]() 和
和![]() 的中点,
的中点,
∴![]() ,
, ![]() ,∴
,∴![]() ,
, ![]() ,
,
则四边形![]() 是平行四边形,则
是平行四边形,则![]() .
.
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() ,∵
,∵![]() 为等边三角形, ∴
为等边三角形, ∴![]() .
.
又![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,
,
建立以![]() 为坐标原点,
为坐标原点, ![]() 分别为
分别为![]() 轴的空间直角坐标系如图:
轴的空间直角坐标系如图:
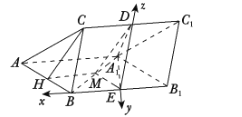
则![]()
![]() ,
, ![]() ,
,
则设平面![]() 的法向量为
的法向量为![]() ,
, ![]() ,
, ![]() ,
,
则![]() ,即
,即
令![]() ,则
,则![]() ,即
,即![]() ,
,
平面![]() 的法向量为
的法向量为![]() ,
, ![]() ,
, ![]() ,
,
则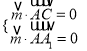 ,得
,得 ,即
,即 ,
,
令![]() ,则
,则![]() ,即
,即![]() ,
,
则![]()

![]() ,
,
即二面角![]() 的余弦值是
的余弦值是![]() .
.

练习册系列答案
相关题目
【题目】某校从参加高三期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及样本频率分布表如下:
分组 | 频数 | 频率 |
[40,50) | 2 | 0.04 |
[50,60) | 3 | 0.06 |
[60,70) | 14 | 0.28 |
[70,80) | 15 | ② |
[80,90) | ① | 0.24 |
[90,100] | 4 | 0.08 |
合计 | ③ | ④ |
(1)请把给出的样本频率分布表中的空格都填上;
(2)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩[90,100]中选两位同学,共同帮助[40,50)中的某一位同学,已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.

