题目内容
在三棱柱 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱 底面
底面 ,点
,点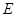 是侧面
是侧面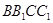 的中心,若
的中心,若 ,则直线
,则直线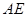 与平面
与平面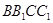 所成角的大小为( )
所成角的大小为( )
A.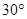 | B.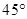 | C. | D.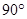 |
A
解析试题分析:由题意画出图形,取BC的中点D,连接AD与ED,因为三棱柱ABC-A1B1C1中,底面是正三角形,侧棱AA1⊥底面ABC,所以平面BCC1B1⊥平面ABC,点E是侧面BB1CC1的中心,所以ED⊥BC,AD⊥BC,所以AD⊥平面EBC,∠AED就是直线AE与平面BB1CC1所成角,∵AA1=3AB,∴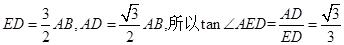 ,所以∠AED=30°,即直线
,所以∠AED=30°,即直线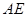 与平面
与平面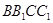 所成角
所成角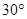 。
。
考点:直线与平面所成的角;正棱柱的结构特征。
点评:本题考查直线与平面垂直的判断方法,直线与平面所成角的求法,考查计算能力.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
如图,面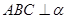 ,
,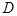 为
为 的中点,
的中点,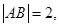
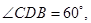
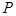 为面
为面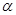 内的动点,且
内的动点,且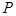 到直线
到直线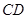 的距离为
的距离为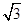 ,则
,则 的最大值( )
的最大值( )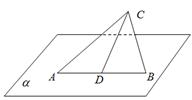
A. | B. | C. | D.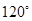 |
设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题中正确的是
| A.若m∥n,m∥α,则n∥α | B.若α⊥β,m∥α,则m⊥β |
| C.若α⊥β,m⊥β,则m∥α | D.若m⊥n,m⊥α, n⊥β,则α⊥β |
设 是两不同直线,
是两不同直线, 是两不同平面,则下列命题错误的是
是两不同平面,则下列命题错误的是
A.若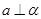 , ,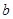 ∥ ∥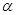 ,则 ,则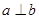 |
B.若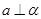 , ,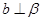 , ,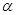 ∥ ∥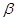 ,则 ,则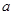 ∥ ∥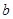 |
C.若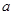 ∥ ∥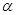 , ,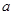 ∥ ∥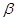 则 则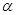 ∥ ∥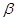 |
D.若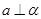 , ,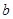 ∥ ∥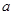 , ,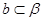 ,则 ,则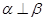 |
若α、β是两个不同的平面,m、n是两条不同直线,则下列命题不正确的是
| A.α∥β,m⊥α,则m⊥β |
| B.m∥n,m⊥α,则n⊥α |
| C. n∥α,n⊥β,则α⊥β |
D.α β=m,n与α、β所成的角相等,则m⊥n β=m,n与α、β所成的角相等,则m⊥n |
设 、b是两条不同的直线,
、b是两条不同的直线, 、
、 是两个不同的平面,则下列四个命题中正确的是( )
是两个不同的平面,则下列四个命题中正确的是( )
A.若 ⊥b, ⊥b, ⊥ ⊥ ,则b∥ ,则b∥ | B.若 ∥ ∥ , , ⊥ ⊥ ,则 ,则 ⊥ ⊥ |
C.若 ⊥ ⊥ , , ⊥ ⊥ ,则 ,则  ∥ ∥ | D.若 ⊥b, ⊥b, ⊥ ⊥ ,b⊥ ,b⊥ ,则 ,则 ⊥ ⊥ |
设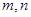 是两条不同的直线,
是两条不同的直线, 是三个不同的平面.给出下列四个命题:
是三个不同的平面.给出下列四个命题:
①若 ⊥
⊥ ,
,  ,则
,则 ;
;
②若 ,则
,则 ;
;
③若 ,则
,则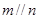 ;
;
④若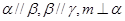 ,则
,则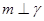 .
.
其中正确命题的序号是( )
| A.①和② | B.②和③ | C.③和④ | D.①和④ |
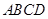 沿对角线
沿对角线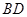 折成直二面角
折成直二面角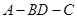 ,有如下四个结论:
,有如下四个结论: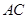 ⊥
⊥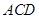 是等边三角形;
是等边三角形;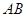 与平面
与平面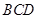 所成的角为60°; ④
所成的角为60°; ④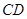 所成的角为60°.
所成的角为60°.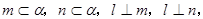 则l⊥α
则l⊥α