题目内容
设m、n是两条不同的直线,α、β是两个不同的平面,则下列命题中正确的是
| A.若m∥n,m∥α,则n∥α | B.若α⊥β,m∥α,则m⊥β |
| C.若α⊥β,m⊥β,则m∥α | D.若m⊥n,m⊥α, n⊥β,则α⊥β |
D
解析试题分析:解:A选项不正确,因为n?α是可能的;
B选项不正确,因为α⊥β,m∥α时,m∥β,m?β都是可能的;
C选项不正确,因为α⊥β,m⊥β时,可能有m?α;
D选项正确,可由面面垂直的判定定理证明其是正确的.
故选D
考点:命题的真假判断与应用
点评:本题考查线面平行、线面垂直以及面面垂直的判断,主要考查空间立体的感知能力以及组织相关知识进行判断证明的能力,属基础题.

练习册系列答案
相关题目
在正三棱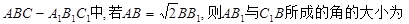 ( )
( )
A.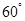 | B.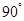 | C.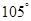 | D.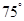 |
已知两个不同的平面α, 和两条不重合的直线m,n,则下列四种说法正确的为( )
和两条不重合的直线m,n,则下列四种说法正确的为( )
A.若m∥n,n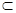 α,则m∥α α,则m∥α |
| B.若m⊥n,m⊥α,则n∥α |
C.若m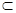 α,n α,n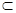  ,α∥ ,α∥ ,则m,n为异面直线 ,则m,n为异面直线 |
D.若α⊥ ,m⊥α,n⊥ ,m⊥α,n⊥ ,则m⊥n ,则m⊥n |
正方体的一条对角线与正方体的棱可组成n对异面直线,则n等于 ( )
| A.2 | B.3 | C.6 | D.12 |
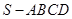 的底面边长为
的底面边长为 ,高
,高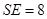 ,点
,点 在高
在高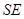 上,且
上,且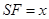 ,记过点
,记过点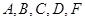 的球的半径为
的球的半径为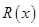 ,则函数
,则函数
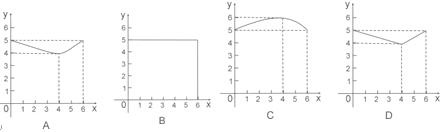
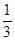
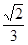
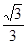
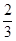
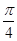 和
和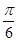 ,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )
,过A、B分别作两平面交线的垂线,垂足为A′、B′,则AB∶A′B′= ( )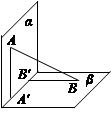
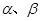 和两条不重合的直线
和两条不重合的直线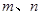 ,有下列四个命题:
,有下列四个命题: //
// ,
,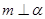 ,则
,则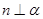 ; ②若
; ②若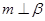 ,则
,则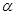 //
//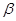 ;
; ,则
,则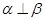 ; ④若
; ④若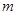 //
// 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱 底面
底面 ,点
,点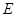 是侧面
是侧面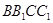 的中心,若
的中心,若 ,则直线
,则直线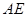 与平面
与平面