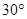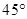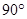题目内容
将正方形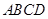 沿对角线
沿对角线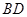 折成直二面角
折成直二面角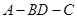 ,有如下四个结论:
,有如下四个结论:
①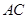 ⊥
⊥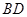 ; ②△
; ②△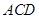 是等边三角形;
是等边三角形;
③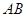 与平面
与平面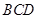 所成的角为60°; ④
所成的角为60°; ④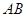 与
与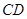 所成的角为60°.
所成的角为60°.
其中错误的结论是( )
| A.① | B.② | C.③ | D.④ |
C
解析试题分析:根据题意可知,当折叠后可知,取BD的中点E,BD与平面ACE垂直,因此可知①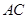 ⊥
⊥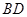 成立。对于②利用三角形AEC是直角三角形可知,该△
成立。对于②利用三角形AEC是直角三角形可知,该△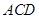 是等边三角形成立。对于③
是等边三角形成立。对于③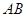 与平面
与平面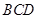 所成的角为45°,也就是角ABD的大小,故错误。
所成的角为45°,也就是角ABD的大小,故错误。
对于④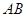 与
与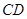 所成的角为60°.那么利用平移法可知成立。故选C.
所成的角为60°.那么利用平移法可知成立。故选C.
考点:本试题考查了折叠图知识。
点评:根据三棱锥的性质可知给定的线面角,以及异面直线的所成的角的大小,解决该试题的关进是对于折叠图前后的不变量,尤其是垂直的运用,属于中档题。

练习册系列答案
相关题目
在正三棱柱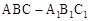 中,若AB=2,
中,若AB=2,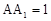 则点A到平面
则点A到平面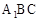 的距离为( )
的距离为( )
A.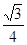 | B. | C.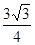 | D. |
已知两个不同的平面α, 和两条不重合的直线m,n,则下列四种说法正确的为( )
和两条不重合的直线m,n,则下列四种说法正确的为( )
A.若m∥n,n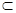 α,则m∥α α,则m∥α |
| B.若m⊥n,m⊥α,则n∥α |
C.若m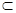 α,n α,n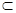  ,α∥ ,α∥ ,则m,n为异面直线 ,则m,n为异面直线 |
D.若α⊥ ,m⊥α,n⊥ ,m⊥α,n⊥ ,则m⊥n ,则m⊥n |
设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
A.若m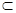 α,n α,n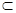 β,m∥n,则α∥β β,m∥n,则α∥β |
| B.若n⊥α,n⊥β,m⊥β,则m⊥α |
| C.若m∥α,n∥β,m⊥n,则α⊥β |
| D.若α⊥β,n⊥β,m⊥n,则m⊥α |
若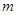 、
、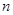 是两条不同的直线,
是两条不同的直线,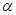 、
、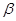 是两个不同的平面,则下列命题中不正确的是( )
是两个不同的平面,则下列命题中不正确的是( )
A.若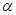 ∥ ∥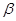 , ,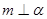 ,则 ,则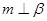 |
B.若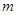 ∥ ∥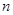 , ,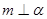 ,则 ,则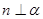 |
C.若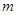 ∥ ∥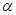 , ,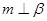 ,则 ,则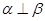 |
D.若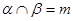 , ,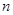 与 与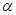 、 、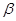 所成的角相等,则 所成的角相等,则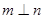 |
已知正四棱柱 中,
中, ,E为
,E为 中点,则异面直线BE与
中点,则异面直线BE与 所成角的余弦值为( )
所成角的余弦值为( )
A. | B. | C. | D. |
已知直线 、
、 、
、 不重合,平面
不重合,平面 、
、 不重合,下列命题正确的是( )
不重合,下列命题正确的是( )
A.若 , , , , ,则 ,则 |
B.若 , , ,则 ,则 |
C.若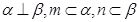 ,则 ,则 |
D.若 ,则 ,则 |
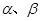 和两条不重合的直线
和两条不重合的直线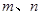 ,有下列四个命题:
,有下列四个命题: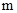 //
// ,
,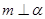 ,则
,则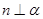 ; ②若
; ②若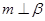 ,则
,则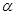 //
//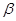 ;
; ,则
,则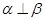 ; ④若
; ④若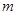 //
// 中,底面是正三角形,侧棱
中,底面是正三角形,侧棱 底面
底面 ,点
,点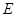 是侧面
是侧面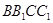 的中心,若
的中心,若 ,则直线
,则直线 与平面
与平面