题目内容
(12分)已知函数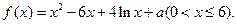 (1)求函数的单调区间;(2)
(1)求函数的单调区间;(2)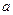 为何值时,方程
为何值时,方程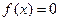 有三个不同的实根.
有三个不同的实根.
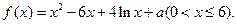 (1)求函数的单调区间;(2)
(1)求函数的单调区间;(2)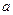 为何值时,方程
为何值时,方程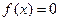 有三个不同的实根.
有三个不同的实根.(Ⅰ) 函数的单调递增区间为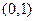 和
和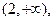 单调递减区间为
单调递减区间为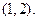
(Ⅱ)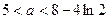
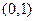 和
和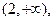 单调递减区间为
单调递减区间为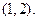
(Ⅱ)
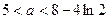
(1)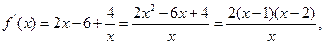 则
则
所以函数的单调递增区间为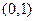 和
和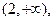 单调递减区间为
单调递减区间为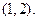
(2)由(1)可知即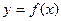 的图像与
的图像与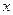 轴有3个不同的交点
轴有3个不同的交点
又知当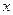 趋近于0时,
趋近于0时,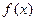 趋近于
趋近于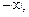
数形结合得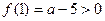 且
且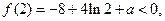
所以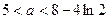
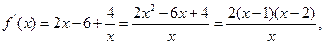 则
则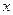 | 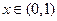 | 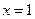 | 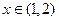 | 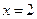 | 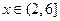 |
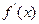 | 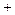 | 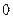 | 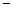 | 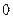 | 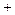 |
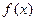 | 递增 | 最大值 | 递减 | 最小值 | 递增 |
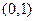 和
和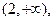 单调递减区间为
单调递减区间为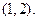
(2)由(1)可知即
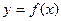 的图像与
的图像与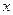 轴有3个不同的交点
轴有3个不同的交点又知当
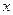 趋近于0时,
趋近于0时,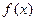 趋近于
趋近于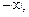
数形结合得
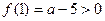 且
且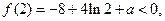
所以
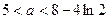

练习册系列答案
相关题目
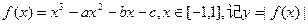 的最大值为M。
的最大值为M。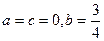 时,求M的值。
时,求M的值。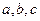 取遍所有实数时,求M的最小值
取遍所有实数时,求M的最小值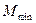 ;
;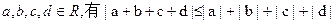 ,当
,当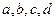 同号时取等号)
同号时取等号)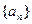 满足
满足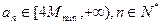 ,求证:
,求证: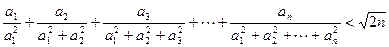 。
。 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .(Ⅰ)求
.(Ⅰ)求 的值;(Ⅱ)若方程
的值;(Ⅱ)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(Ⅲ)令
为自然对数的底数);(Ⅲ)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 ,
, (其中
(其中 ),
), 的中点为
的中点为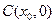 ,求证:
,求证: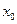 处的导数
处的导数 .
.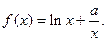
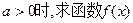 的单调区间;
的单调区间;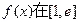 上的最小值为1,求实数a的取值范围;(其中e为自然对数的底数)
上的最小值为1,求实数a的取值范围;(其中e为自然对数的底数)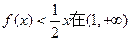 上恒成立,求实数a的取值范围。
上恒成立,求实数a的取值范围。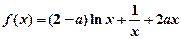 (a∈R).
(a∈R).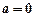 时,求
时,求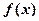 的极值;
的极值;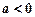 时,求
时,求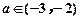 及
及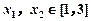 ,恒有
,恒有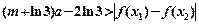
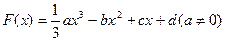 的图象过原点,
的图象过原点,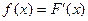 ,
,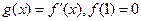 ,函数y=f(x)与y=g(x)的图象交于不同两点A、B。
,函数y=f(x)与y=g(x)的图象交于不同两点A、B。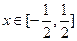 ,求线段AB在x轴上的射影长的取值范围;
,求线段AB在x轴上的射影长的取值范围;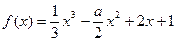 且
且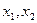 是
是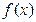 的两个极值点,
的两个极值点,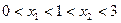 ,
,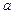 的取值范围;
的取值范围;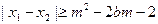 ,对
,对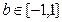 恒成立。求实数
恒成立。求实数 的取值范围;
的取值范围;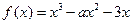 ,
,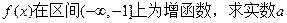 的取值范围;
的取值范围; 的图象与
的图象与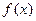 的图象恰有3个交点?若存在求出
的图象恰有3个交点?若存在求出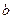 的取值范围;若不存在,试说明理由.
的取值范围;若不存在,试说明理由.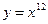 ;(2)
;(2)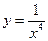 ;(3)
;(3)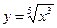 .
.