题目内容
(本小题满分14分) 已知函数 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .(Ⅰ)求
.(Ⅰ)求 的值;(Ⅱ)若方程
的值;(Ⅱ)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(Ⅲ)令
为自然对数的底数);(Ⅲ)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 ,
, (其中
(其中 ),
), 的中点为
的中点为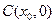 ,求证:
,求证: 在
在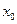 处的导数
处的导数 .
.
 图象上一点
图象上一点 处的切线方程为
处的切线方程为 .(Ⅰ)求
.(Ⅰ)求 的值;(Ⅱ)若方程
的值;(Ⅱ)若方程 在
在 内有两个不等实根,求
内有两个不等实根,求 的取值范围(其中
的取值范围(其中 为自然对数的底数);(Ⅲ)令
为自然对数的底数);(Ⅲ)令 ,若
,若 的图象与
的图象与 轴交于
轴交于 ,
, (其中
(其中 ),
), 的中点为
的中点为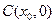 ,求证:
,求证: 在
在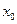 处的导数
处的导数 .
.(Ⅰ) 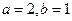 (Ⅱ)
(Ⅱ) 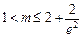 (Ⅲ)见解析
(Ⅲ)见解析
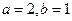 (Ⅱ)
(Ⅱ) 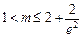 (Ⅲ)见解析
(Ⅲ)见解析(Ⅰ)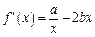 ,
, ,
,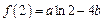 .
.
∴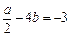 ,且
,且 . …………………… 2分
. …………………… 2分
解得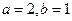 .……… 3分
.……… 3分
(Ⅱ) ,令
,令 ,
,
则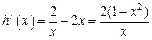 ,令
,令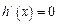 ,得
,得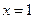 (
(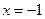 舍去).
舍去).
在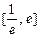 内,当
内,当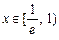 时,
时, , ∴
, ∴ 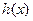 是增函数;
是增函数;
当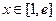 时,
时,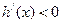 , ∴
, ∴ 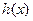 是减函数 ……………… 5分
是减函数 ……………… 5分
则方程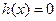 在
在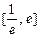 内有两个不等实根的充要条件是
内有两个不等实根的充要条件是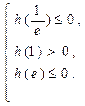 ……6分
……6分
即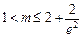 .…… 8分
.…… 8分
(Ⅲ)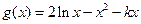 ,
, .
.
假设结论不成立,则有 …… 9分
…… 9分
①-②,得 .∴
.∴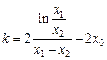 .…… 10分
.…… 10分
由④得 ,∴
,∴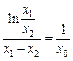 …… 11分
…… 11分
即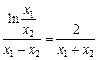 ,即
,即 .⑤
.⑤
令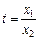 ,
, (
( ), … 12分
), … 12分
则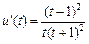 >0.∴
>0.∴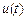 在
在 上增函数, ∴
上增函数, ∴ ,… 13分
,… 13分
∴⑤式不成立,与假设矛盾.∴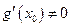 .… 14分
.… 14分
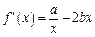 ,
, ,
,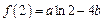 .
.∴
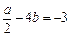 ,且
,且 . …………………… 2分
. …………………… 2分解得
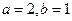 .……… 3分
.……… 3分(Ⅱ)
 ,令
,令 ,
,则
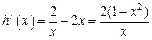 ,令
,令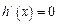 ,得
,得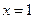 (
(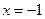 舍去).
舍去).在
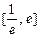 内,当
内,当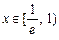 时,
时, , ∴
, ∴ 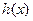 是增函数;
是增函数;当
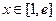 时,
时,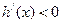 , ∴
, ∴ 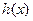 是减函数 ……………… 5分
是减函数 ……………… 5分则方程
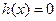 在
在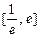 内有两个不等实根的充要条件是
内有两个不等实根的充要条件是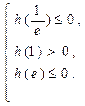 ……6分
……6分即
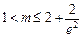 .…… 8分
.…… 8分(Ⅲ)
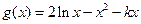 ,
, .
.假设结论不成立,则有
 …… 9分
…… 9分①-②,得
 .∴
.∴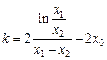 .…… 10分
.…… 10分由④得
 ,∴
,∴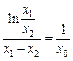 …… 11分
…… 11分即
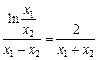 ,即
,即 .⑤
.⑤ 令
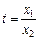 ,
, (
( ), … 12分
), … 12分则
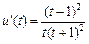 >0.∴
>0.∴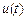 在
在 上增函数, ∴
上增函数, ∴ ,… 13分
,… 13分∴⑤式不成立,与假设矛盾.∴
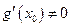 .… 14分
.… 14分
练习册系列答案
相关题目
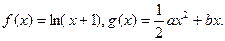
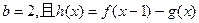 存在单调递减区间,求
存在单调递减区间,求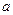 的取值范围;
的取值范围;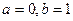 时,求证
时,求证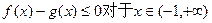 成立;
成立;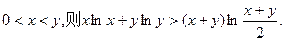
 。
。 ,证明:
,证明: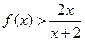 ;
; 对
对 时恒成立,求实数
时恒成立,求实数 的取值范围。
的取值范围。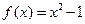 与函数
与函数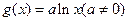 .
.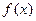 ,
,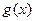 的图像在点
的图像在点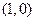 处有公共的切线,求实数
处有公共的切线,求实数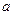 的值;
的值;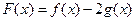 ,求函数
,求函数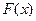 的值.
的值.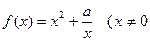 ,常数
,常数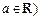 .
.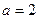 时,解不等式
时,解不等式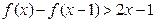 ;
;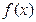 的奇偶性,并说明理由.
的奇偶性,并说明理由.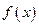 在
在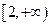 是增函数,求实数
是增函数,求实数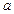 的范围
的范围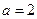 ,求过点
,求过点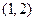 处的切线方程;
处的切线方程; 是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由.
是否为“Storm函数”?如果是,请给出证明;如果不是,请说明理由. (1)求函数的单调区间;(2)
(1)求函数的单调区间;(2)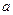 为何值时,方程
为何值时,方程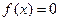 有三个不同的实根.
有三个不同的实根.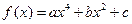 的图象过点
的图象过点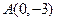 ,且它在
,且它在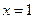 处的切线方程为
处的切线方程为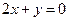 .
.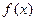 的解析式;
的解析式;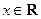 ,不等式
,不等式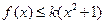 恒成立,求实数
恒成立,求实数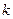 的取值范围.
的取值范围. .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 在区间
在区间 上零点的个数.
上零点的个数.